
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Representing graphs
One way to represent a graph without multiple edges is to list all the edges of this graph. Another way to represent a graph with no multiple edges is to use adjacency lists, which specify the vertices that are adjacent to each vertex of the graph.
Example. Use adjacency lists to describe the simple graph given in Figure below.
 Solution:
Solution:
| An edge list for a simple graph | |
| Vertex | Adjacent vertices |
| a b c d e | b, c, e a a, d, e c, e a, c, d |
Example. Represent the directed graph by listing all the vertices that are the terminal vertices of edges starting at each vertex of the graph.
 Solution:
Solution:
| An edge list for a directed graph | |
| Initial vertex | Terminal vertex |
| a b c d e | b, c, d, e b, d a, c, e b, c, d |
Adjacency matrices
Suppose that 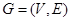 is a simple graph where
is a simple graph where 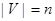 . Suppose that the vertices of G are listed arbitrarily as
. Suppose that the vertices of G are listed arbitrarily as 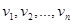 . The adjacency matrix A (or AG) of G, with respect to this listing of the vertices, is the
. The adjacency matrix A (or AG) of G, with respect to this listing of the vertices, is the 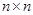 zero-one matrix with 1 as its (i, j)th entry when vi and vj are adjacent, and 0 as its (i, j)th entry when they are not adjacent. In other words, if its adjacency matrix is
zero-one matrix with 1 as its (i, j)th entry when vi and vj are adjacent, and 0 as its (i, j)th entry when they are not adjacent. In other words, if its adjacency matrix is 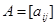 , then
, then 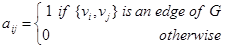 .
.
Example. Use an adjacency matrix to represent the graph shown in Figure below.
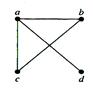
Solution: We order the vertices as a, b, c, d. The matrix representing this graph is  .
.
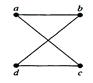
Example. Draw a graph with the adjacency matrix 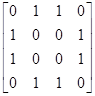 with respect to the ordering of vertices a, b, c, d.
with respect to the ordering of vertices a, b, c, d.
Solution:
Adjacency matrices can also be used to represent undirected graphs with loops and with multiple edges. A loop at the vertex ai is represented by a 1 at the (i, i)th position of the adjacency matrix. When multiple edges are present, the adjacency matrix is no longer a zero-one matrix, since the (i, j)th entry of this matrix equals the number of edges that are associated to 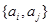 .
.
Example. Use an adjacency matrix to represent the pseudograph shown in Figure below.
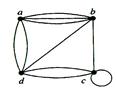
Solution: The adjacency matrix using the ordering of vertices a, b, c, d is  .
.
Date: 2015-01-02; view: 1537
| <== previous page | | | next page ==> |
| Bipartite graphs | | | Incidence matrices |