Some special simple graphs

A partially ordered set in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice.

Example. Determine whether the posets represented by each of the Hasse diagrams in Figure below are lattices.

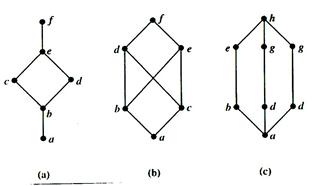
Solution: The posets represented by the Hasse diagrams in (a) and (c) are both lattices because in each poset every pair of elements has both a least upper bound and a greatest lower bound. On the other hand, the poset with the Hasse diagram shown in (b) is not a lattice, since the elements b and c have no least upper bound. To see this note that each of the elements d, e and f is an upper bound, but none of these three elements precedes the other two with respect to the ordering of this poset.

Glossary

equivalence relation – отношение эквивалентности; partition – разбиение

partial order – частичный порядок; linear order – линейный порядок

well-ordered set – вполне упорядоченное множество; bound – граница

lattice – решетка

Graphs

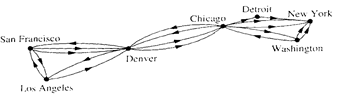
We will introduce the different types of graphs by showing how each can be used to model a computer network. Suppose that a network is made up of computers and telephone lines between computers. We can represent the location of each computer by a point and each telephone line by an arc, as shown in Figure below.

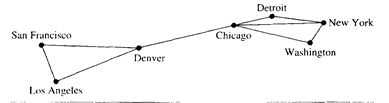
There is at most one telephone line between two computers in this network, each line operates in both directions, and no computer has a telephone line to itself. Consequently, this network can be modeled using a simple graph, consisting of vertices that represent the computers and undirected edges that represent telephone lines, where each edge connects two distinct vertices and no two edges connect the same pair of vertices.

A simple graph consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V, called edges.

Sometimes there are multiple telephone lines between computers in a network. This is the case when there is a heavy traffic between computers. A network with multiple lines is displayed in Figure below.

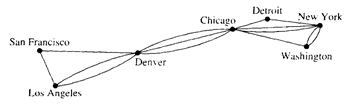
Simple graphs are not sufficient to model such networks. Instead, multigraphs are used, which consists of vertices and undirected edges between these vertices, with multiple edges between vertices allowed. Every simple graph is also a multigraph. However, not all multigraphs are simple graphs, since in multigraph two or more edges may connect the same pair of vertices.

A multigraph consists of a set V of vertices, a set E of edges, and a function f from E to 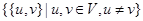. The edges e₁ and e₂ are called multiple or parallel edges if .

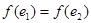A computer network may connect a telephone line from a computer to itself (perhaps for diagnostic purposes). Such a network is shown in Figure below.

We cannot use multigraphs to model such networks, since loops, which are edges from a vertex to itself, are not allowed in multigraphs. Instead, pseudographs are used.

A pseudograph consists of a set V of vertices, a set E of edges, and a function f from E to 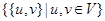. An edge is a loop if 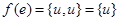for some .

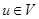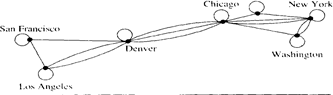
The telephone lines in a computer network may not operate in both directions. For instance, in Figure below the host computer in New York can only receive data from other computers and cannot send out data. The other telephone lines operate in both directions and are represented by pairs of edges in opposite directions.

A directed graph consists of a set V of vertices and a set E of edges that are ordered pairs of elements of V. In a directed graph loops, ordered pairs of the same element, are allowed, but multiple edges in the same direction between two vertices are not.

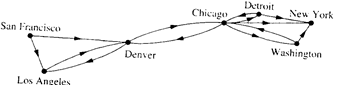
Finally, multiple lines may be present in the computer network, so that there may be several one-way lines to the host in New York from each location, and perhaps more than one line back to each remote computer from the host.

A directed multigraph consists of a set V of vertices, a set E of edges, and a function f from E to 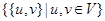. The edges e₁ and e₂ are called multiple edges if .

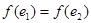Two vertices u and v in an undirected graph G are called adjacent (or neighbors) in G if {u, v} is an edge of G. If e = {u, v}, the edge e is called incident with the vertices u and v. The edge e is also said to connect u and v. The vertices u and v are called endpoints of the edge {u, v}.

The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex v is denoted by deg(v).

Example. What are the degrees of the vertices in the graph G and H?

Solution: In G, deg(a) = 2, deg(b) = deg(c) = deg(f) = 4, deg(d) = 1, deg(e) = 3 and deg(g) = 0.

In H, deg(a) = 4, deg(b) = deg(e) = 6, deg(c) = 1 and deg(d) = 5.

A vertex of degree 0 is called isolated. A vertex is pendant iff it has degree 1.

What do we get when we add the degrees of all the vertices of a graph ? Each edge contributes 2 to the sum of the degrees of the vertices since an edge is incident with exactly two (possibly equal) vertices. This means that the sum of the degrees of the vertices is twice the number of edges. We the following result, which is sometimes called the Handshaking Theorem, because of the analogy between an edge having two endpoints and a handshake involving two hands.

Theorem 1 (The Handshaking Theorem). Let be an undirected graph with e edges. Then 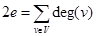. (Note that this applies even if multiple edges and loops are present.)

Example. How many edges are there in a graph with 10 vertices each of degree 6?

Solution: Since the sum of the degrees of the vertices is 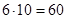, it follows that 2e = 60. Therefore, e = 30.

Theorem 2. An undirected graph has an even number of vertices of odd degree.

Proof: Let V₁ and V₂ be the set of vertices of even degree and the set of vertices of odd degree, respectively, in an undirected graph . Then 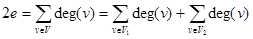. Since deg(v) is even for 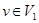, the first term in the right-hand side of the last equality is even. Furthermore, the sum of the two terms on the right-hand side of the last equality is even, since this sum is 2e. Hence, the second term in the sum is also even. Since all the terms in this sum are odd, there must be an even number of such terms. Thus, there is an even number of vertices of odd degree.

When (u, v) is an edge of the graph G with directed edges, u is said to be adjacent to v and v is said to be adjacent from u. The vertex u is called the initial vertex of (u, v), and v is called the terminal or end vertex of (u, v). The initial vertex and terminal vertex of a loop are the same.

In a graph with directed edges the in-degree of a vertex v, denoted by 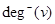, is the number of edges with v as their terminal vertex. The out-degree of v, denoted by 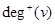, is the number of edges with v as their initial vertex. Note that a loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex.

Example. Find the in-degree and out-degree of each vertex in the graph G with directed edges.

Solution: , , , , ;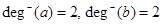

, , , , .

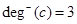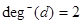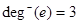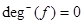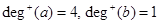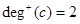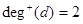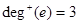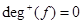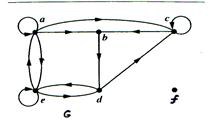
Since each edge has an initial vertex and a terminal vertex, the sum of the in-degrees and the sum of the out-degrees of all vertices in a graph with directed edges are the same. Both of these sums are the number of edges in the graph. This result is stated as the following theorem.

Theorem 3. Let be a graph with directed edges. Then .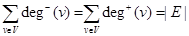

Some special simple graphs

Example. The complete graph on n vertices, denoted by K_n, is the simple graph that contains exactly one edge between each pair of distinct vertices.

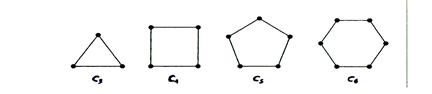
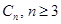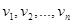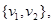
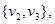
Example. The cycle , consists of n vertices and edges and .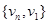

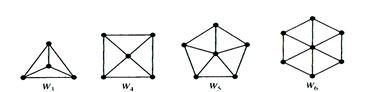
Example. We obtain the wheel W_n when we add an additional vertex to the cycle C_n, for , and connect this new vertex to each of the n vertices in C_n, by new edges.

Example. The n-cube, denoted by Q_n, is the graph that has vertices representing the 2ⁿ bit strings of length n. Two vertices are adjacent iff the bit strings that they represent differ in exactly one bit position.

Date: 2015-01-02; view: 2514