Maximal and minimal elements

Elements of a poset that have certain extremal properties are important for many applications. An element a of a poset 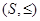is called maximal if there is no 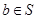such that 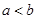. An element a of a poset 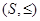is called minimal if there is no 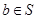such that .

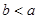Example. Which elements of the poset 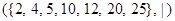are maximal, and which are minimal?

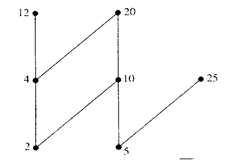
Solution: The Hasse diagram for this poset shows that the maximal elements are 12, 20 and 25, and the minimal elements are 2 and 5. As this example shows, a poset can have more than one maximal element and more than one minimal element.

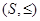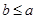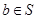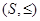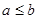Sometimes there is an element in a poset that is greater (or less) than every other element. An element a is called the greatest element of the poset if for all . The greatest element is unique when it exists. Likewise, an element a is called the least element of if for all 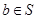. The least element is unique when it exists.

Example. Determine whether the posets represented by each of the Hasse diagrams in Figure below have a greatest element and a least element.

Solution: The least element of the poset with Hasse diagram (a) is a. This poset has no greatest element. The poset with Hasse diagram (b) has neither a least nor a greatest element. The poset with Hasse diagram (c) has no least element. Its greatest element is d. The poset with Hasse diagram (d) has least element a and greatest element d.

Sometimes it is possible to find an element that is greater than all the elements in a subset A of a poset (S, £). If u is an element of S such that a £ u for all elements a Î A, then u is called an upper bound of A. Likewise, there may be an element less than all the elements in A. If l is an element of S such that l £ a for all elements a Î A, then l is called a lower bound of A.

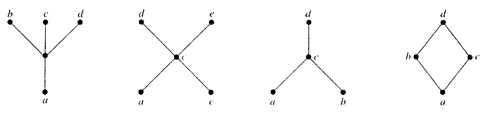
Example. Find the lower and upper bounds of the subsets {a, b, c}, {j, h} and {a, c, d, f} in the poset with the Hasse diagram shown in Figure below.

Solution: The upper bounds of {a, b, c} are e, f, j and h, ant its only lower bound is a. There no upper bounds of {j, h} and its lower bounds are a, b, c, d, e and f. The upper bounds of {a, c, d, f} are f, h and j, and its lower bound is a.

The element x is called the least upper bound of a subset A if x is an upper bound that is less than every other upper bound of A. That is, x is the least upper bound of A if a £ x whenever a Î A, and x £ z whenever z is an upper bound of A. The least upper bound of A (lub(A)) is unique if it exists. Similarly, the element y is called the greatest lower bound of A if y is a lower bound of A and z £ y whenever z is a lower bound of A. The greatest lower bound of A (glb(A)) is unique if it exists.

Example. Find the greatest lower bound and the least upper bound of {b, d, g}, if they exist, in the poset shown in Figure above.

Solution: The upper bounds of {b, d, g} are g and h. Since g < h, g is the least upper bound. The lower bounds of {b, d, g} are a and b. Since a < b, b is the greatest lower bound.

Date: 2015-01-02; view: 5141