Hasse diagrams

Many edges in the directed graph for a finite poset do not have to be shown since they must be present. For instance, consider the directed graph for the partial ordering 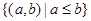on the set {1, 2, 3, 4}, shown in Figure 1(a). Since this relation is a partial ordering, it is reflexive, and its directed graph has loops at all vertices. Consequently, we do not have to show these loops since they must be present; in Figure 1(b) loops are not shown. Because a partial ordering is transitive, we do not have to show those edges that must be present because of transitivity. For example, in Figure 1(c) the edges (1, 3), (1, 4) and (2, 4) are not shown since they must be present. If we assume that all edges are pointed “upward” (as they are drawn in the figure), we do not have to show the directions of the edges; Figure 1(c) does not show directions. It is called the Hasse diagram for ({1, 2, 3, 4}, £).

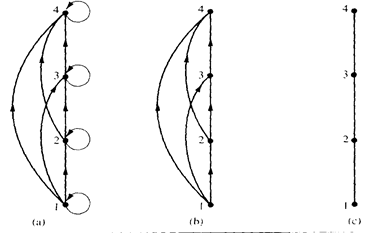
Example. Draw the Hasse diagram for the partial ordering {(A, B) | A Í B} on the power set P(S) where S = {a, b, c}.

Solution: The Hasse diagram for this partial ordering is obtained from the associated digraph by deleting all the loops and all the edges that occur from transitivity, namely, (Æ, {a, b}), (Æ, {a, c}), (Æ, {b, c}), (Æ, {a, b, c}), ({a}, {a, b, c}), ({b}, {a, b, c}), and ({c}, {a, b, c}). Finally all edges point upward and arrows are deleted. The resulting Hasse diagram is illustrated in Figure below.

Date: 2015-01-02; view: 1619