
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Lexicographic order
The words in a dictionary are listed in alphabetic, or lexicographic, order, which is based on the ordering of the letters in the alphabet. This is a special case of an ordering of strings on a set constructed from a partial ordering on the set.
The lexicographic ordering 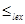 on
on 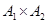 is defined by specifying that one pair is less than a second pair if the first entry of the first pair isles than (in A1) the first entry of the second pair, or if the first entries are equal, but the second entry of this pair is less than (in A2) the second entry of the second pair. In other words,
is defined by specifying that one pair is less than a second pair if the first entry of the first pair isles than (in A1) the first entry of the second pair, or if the first entries are equal, but the second entry of this pair is less than (in A2) the second entry of the second pair. In other words, 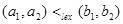 , either if
, either if 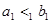 or if both
or if both 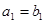 and
and 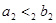 . We obtain a partial ordering
. We obtain a partial ordering 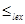 by adding equality to the ordering
by adding equality to the ordering 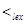 on
on 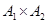 .
.
Example. Determine whether 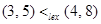 , whether
, whether 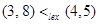 , whether
, whether 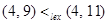 in the poset
in the poset 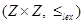 , where
, where 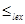 is the lexicographic ordering constructed from the usual ≤ relation on Z.
is the lexicographic ordering constructed from the usual ≤ relation on Z.
A lexicographic ordering can be defined on the Cartesian product of n posets 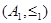 ,
, 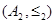 , …,
, …, 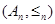 . Define the partial ordering
. Define the partial ordering 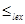 on
on 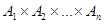 by
by 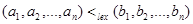 if
if 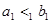 , or if there is an integer
, or if there is an integer 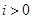 such that
such that 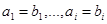 and
and 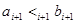 .
.
We can now define lexicographic ordering of strings. Consider the strings 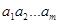 and
and 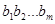 on a partially ordered set S. Suppose these strings are not equal. Let t be the minimum of m and n. The definition of lexicographic ordering is that the string
on a partially ordered set S. Suppose these strings are not equal. Let t be the minimum of m and n. The definition of lexicographic ordering is that the string 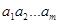 is less than
is less than 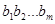 iff
iff 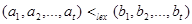 or
or 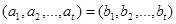 and m < n where
and m < n where 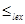 in this inequality represents the lexicographic ordering of S t.
in this inequality represents the lexicographic ordering of S t.
Example. Consider the set of strings of lowercase English letters. Using the ordering of letters in the alphabet, a lexicographic ordering on the set of strings can be constructed. A string is less than a second string if the letter in the first string in the first position where the strings differ comes before the letter in the second string in this position, or if the first string and the second string agree in all positions, but the second string has more letters. This ordering is the same as that used in dictionaries. For example, discreet 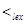 discrete, since these strings differ first in the seventh position, and e
discrete, since these strings differ first in the seventh position, and e 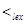 t. Also, discreet
t. Also, discreet 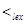 discreetness, since the first eight letters agree, but the second string is longer. Furthermore, discrete
discreetness, since the first eight letters agree, but the second string is longer. Furthermore, discrete 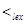 discretion, since discrete
discretion, since discrete 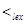 discreti.
discreti.
Date: 2015-01-02; view: 1423
| <== previous page | | | next page ==> |
| Partial orderings | | | Hasse diagrams |