Partial orderings

A relation R on a set S is called a partial ordering or partial order if it is reflexive, antisymmetric and transitive. A set S together with a partial ordering R is called a partially ordered set, or poset, and is denoted by (S, R).

Example. Show that the “greater than or equal” relation ≥ is a partial ordering on the set of integers.

Solution: Since 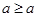for every integer a, ≥ is reflexive. If 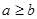and 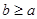, then a = b. Hence, ≥ is antisymmetric. Finally, ≥ is transitive since 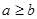and 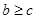imply that 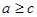. It follows that ≥ is a partial ordering on the set of integers and 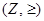is a poset.

Example. The divisibility relation | is a partial ordering on the set of positive integers, since it is reflexive, antisymmetric and transitive. We see that 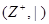is a poset ( 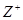denotes the set of positive integers).

Example. Show that the inclusion relation Í is a partial ordering on the power set of a set S.

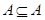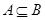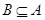Solution: Since whenever A is a subset of S, Í is reflexive. It is antisymmetric since and imply that A = B. Finally, Í is transitive, since 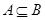and 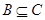imply that 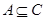. Hence, Í is a partial ordering on P(S), and 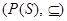is a poset.

In a poset the notation 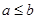denotes that 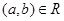. The notation 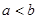denotes tha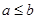t , but 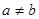. Also, we say “a is less than b” or “b is greater than a” if .

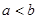The elements a and b of a poset 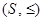are called comparable if eithe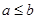r or 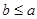. When a and b are elements of S such that neithe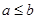r nor 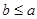, a and b are called incomparable.

Example. In the poset 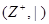, are the integers 3 and 9 comparable? Are 5 and 7 comparable?

Solution: The integers 3 and 9 are comparable, since 3 | 9. The integers 5 and 7 are incomparable, because 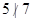and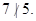

The adjective “partial” is used to describe partial orderings since pairs of elements may be incomparable. When every two elements in the set are comparable, the relation is called a total ordering.

If 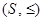is a poset and every two elements of S are comparable, S is called a totally ordered or linearly ordered set, and ≤ is called a total order or a linear order. A totally ordered set is also called a chain.

Example. The poset 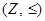is totally ordered, since 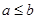or 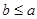whenever a and b are integers.

Example. The poset 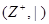is not totally ordered since it contains elements that are incomparable, such as 5 and 7.

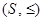is a well-ordered set if it is a poset such that ≤ is a total ordering and such that every nonempty subset of S has a least element.

Example. The set of ordered pairs of positive integers, 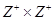, with 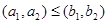if 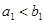, or if 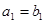and 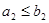(the lexicographic ordering), is a well-ordered set. The set Z, with the usual ≤ ordering, is not well-ordered since the set of negative integers, which is a subset of Z, has no least element.

Date: 2015-01-02; view: 1618