
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Equivalence relations
New England
American manufacturing began in the Northeast. The first factories were in New England. They produced cotton cloth, supplied coal, natural gas, oil and water power to other regions.
Fishing has been important in the Northeast. Many towns began as a fishing community: Boston, Portland, New Bedford and Gloucester.
The Midwest
The eastern part of the Midwest is corn country. This region is called the Corn Belt. Farming is the leading industry.
The northern part of the Midwest is a hay and dairy region. Wisconsin is the leading dairy state.
The drier western parts of the Midwest are wheat lands. There is a big supply of raw materials – iron ore, livestock, wheat, timber, etc.
Meat packing and flour milling are big Midwestern business. Buffalo, at the eastern end of Lake Erie in New York State, is a milling centre. It is cheaper to transport goods by water than by rail.
Detroit is the centre of automobile industry. Over half the motor vehicles and equipment made in the USA comes from the Midwest.
The South
The South is rich in natural resources: sulphur, salt, phosphate, natural gas, iron ore, coal. Birmingham is an important producer of iron and steel. Oil and natural gas help refinery and chemical industry to develop in the South.
The West
The three states of the West Coast – California, Oregon and Washington – have important farm lands. The crops in California are cotton, wheat, rice and barley. Los Angeles is famous for its oil, aircraft and tire manufacturing, automobile assembly plants.
Another West Coast manufacturing centre is the San Francisco Bay area with its food processing, oil refining and electronics.
Answer the questions:
1. What are the main physiographic divisions of the US?
2. Name the main mountain ranges, the highest peaks and the lowest points in the US.
3. What are the major rivers and lakes of the USA?
4. How does the climate vary throughout the country?
5. What natural resources are found in the USA?
6. Can you remember the most important cities and industries developed in the US?
Equivalence relations
A relation on a set A is called an equivalence relation if it is reflexive, symmetric and transitive. Two elements that are related by an equivalence relation are called equivalent.
Example. Suppose that R is the relation on the set of strings of English letters such that aRb iff l(a) = l(b), where l(x) is the length of the string x. Is R an equivalence relation?
Solution: Since l(a) = l(a), it follows that aRa whenever a is a string, so that R is reflexive. Next, suppose that aRb, so that l(a) = l(b). Then bRa, since l(b) = l(a). Hence, R is symmetric. Finally, suppose that aRb and bRc. Then l(a) = l(b) and l(b) = l(c). Hence, l(a) = l(c), so that aRc. Consequently, R is transitive. Since R is reflexive, symmetric and transitive, it is an equivalence relation.
Example (Congruence Modulo m). Let m be a positive integer greater than 1. Show that the relation 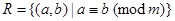 is an equivalence relation on the set of integers.
is an equivalence relation on the set of integers.
Solution: Recall that 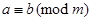 iff m divides a – b. Note that a – a = 0 is divisible by m, since 0 = 0 × m. Hence,
iff m divides a – b. Note that a – a = 0 is divisible by m, since 0 = 0 × m. Hence, 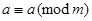 , so that congruence modulo m is reflexive. Now suppose that
, so that congruence modulo m is reflexive. Now suppose that 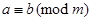 . Then a – b is divisible by m, so that a – b = km, where k is an integer. It follows that b – a = (– k)m, so that
. Then a – b is divisible by m, so that a – b = km, where k is an integer. It follows that b – a = (– k)m, so that 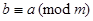 . Hence, congruence modulo m is symmetric. Next, suppose that
. Hence, congruence modulo m is symmetric. Next, suppose that 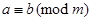 and
and 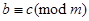 . Then m divides both a – b and b – c. Therefore, there are integers k and l with a – b = km and b – c = lm. Adding these two equations shows that a – c = (a – b) + (b – c) = km + lm = (k + l) m. Thus,
. Then m divides both a – b and b – c. Therefore, there are integers k and l with a – b = km and b – c = lm. Adding these two equations shows that a – c = (a – b) + (b – c) = km + lm = (k + l) m. Thus, 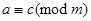 . Therefore, congruence modulo m is transitive. It follows that congruence modulo m is an equivalence relation.
. Therefore, congruence modulo m is transitive. It follows that congruence modulo m is an equivalence relation.
Let R be an equivalence relation on a set A. The set of all elements that are related to an element a of A is called the equivalence class of a. The equivalence class of a with respect to R is denoted by 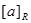 . When only one relation is under consideration, we will delete the subscript R and write
. When only one relation is under consideration, we will delete the subscript R and write 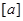 for this class. In other words, if R is an equivalence relation on a set A, the equivalence class of the element a is
for this class. In other words, if R is an equivalence relation on a set A, the equivalence class of the element a is  . If
. If 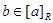 , b is called a representative of this equivalence class.
, b is called a representative of this equivalence class.
Example. What are the equivalence classes of 0 and 1 for congruence modulo 4?
Solution: the equivalence class of 0 contains all integers a such that 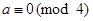 . The integers in this class are those divisible by 4. Hence,
. The integers in this class are those divisible by 4. Hence, 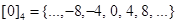 . The equivalence class of 1 contains all the integers a such that
. The equivalence class of 1 contains all the integers a such that 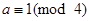 . The integers in this class are those that have a remainder of 1 when divided by 4. Hence,
. The integers in this class are those that have a remainder of 1 when divided by 4. Hence, 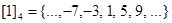 .
.
The equivalence classes of the relation congruence modulo m are called the congruence classes modulo m. The congruence class of an integer a modulo m is denoted by 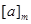 so that
so that
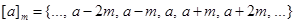 .
.
The following theorem shows that the equivalence classes of two elements of A are either identical or disjoint.
Theorem 1. Let R be an equivalence relation on a set A. The following statements are equivalent:
(i) aRb; (ii) 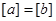 ; (iii)
; (iii) 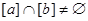 .
.
We are now in a position to show how an equivalence relation partitions a set. Let R be an equivalence relation on a set A. The union of the equivalence classes of R is all of A, since an element a of A is in its own equivalence class, namely, 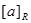 . In other words,
. In other words, 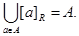
In addition, from Theorem 1, it follows that these equivalence classes are either equal or disjoint, so 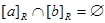 when
when 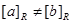 . These two observations show that the equivalence classes form a partition of A, since they split A into disjoint subsets. More precisely, a partition of a set S is a collection of disjoint nonempty subsets of S that have S as their union. In other words, the collection of subsets
. These two observations show that the equivalence classes form a partition of A, since they split A into disjoint subsets. More precisely, a partition of a set S is a collection of disjoint nonempty subsets of S that have S as their union. In other words, the collection of subsets 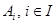 (where I is an index set) forms a partition of S iff
(where I is an index set) forms a partition of S iff 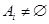 for
for 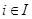 ,
,  when
when 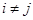 and
and 
Example. Suppose that S = {1, 2, 3, 4, 5, 6}. The collection of sets A1 = {1, 2, 3}, A2 = {4, 5} and A3 = {6} forms a partition of S, since these sets are disjoint and their union is S.
Theorem 2. Let R be an equivalence relation on a set S. Then the equivalence classes of R form a partition of S. Conversely, given a partition 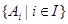 of the set S, there is an equivalence relation R that has the sets
of the set S, there is an equivalence relation R that has the sets 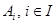 , as its equivalence classes.
, as its equivalence classes.
Example. What are the sets in the partition of the integers arising from congruence modulo 4?
Solution: There are four congruence classes, corresponding to 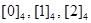 and
and 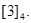 They are the sets
They are the sets 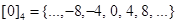 ,
, 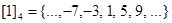 ,
, 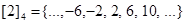 ,
,
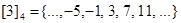 . These congruence classes are disjoint, and every integer is in exactly one of them. In other words, as Theorem 2 says, these congruence classes form a partition.
. These congruence classes are disjoint, and every integer is in exactly one of them. In other words, as Theorem 2 says, these congruence classes form a partition.
Date: 2015-01-02; view: 1651
| <== previous page | | | next page ==> |
| IV The main industries and cities. | | | Partial orderings |