Part 5. Integration of Ordinary Differential Equations

TABLE 5.1 Comparison of the characteristics of alternative methods

Method	Starting Values	Ease of Changing Step Size	Global Error
One step
Euler's		Easy	O(h)
Midpoint		Easy	O(h²)
Fourth – order RK		Easy	O(h⁴)
Multistep
Fourth – order Adams		Difficult	O(h⁵)

TABLE 5.2 Summary of important information

Method	Formulation	Errors
Euler (First – order RK)		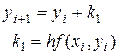Local error @ O(h²) Global error @ O(h)
Midpoint method		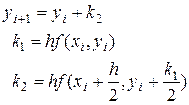Local error @ O(h³) Global error @ O(h²)
Classic fourth – order RK		Local error @ O(h⁵) Global error @ O(h⁴)
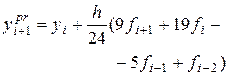
Fourth – order Adams	Predictor: (fourth Adams - Bashforth) Corrector: (fourth Adams - Moulton)	Local error @ O(h⁵) Global error @ O(h⁴)

Example 1

Use Euler's method to numerically integrate: 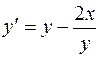from
x = 0 to x = 1 with a step size of: a) h = 0.2, b) h = 0.1. Compute percent relative errors for the numerical results. The initial condition at x = 0 is
y = 1. Recall that the exact solution is given by .

Solution. a)Equation 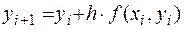can be used to implement Euler's method: the slope estimate at x = 0 and y = 1 is f(0,1) = 1.

Therefore, .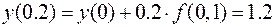

The true solution at x = 0.2 is .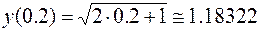

Thus, the error is . The computation is repeated, and the results are compiled in Table 5.3.

TABLE 5.3.

x	y_true	y_Euler	e_t, %
h = 0.2	h = 0.1	h = 0.2	h = 0.1
	1.0	1.0	1.0
0.1	1.095445		1.1		-0.41
0.2	1.183216	1.2	1.191818	-1.4	-0.72
0.3	1.264911		1.277438		-0.98
0.4	1.341641	1.373333	1.358213	-3.2	-1.22
0.5	1.414214		1.435133		-1.46
0.6	1.48324	1.531495	1.508966	-4.8	-1.70
0.7	1.549193		1.580338		-1.97
0.8	1.612452	1.681085	1.649784	-6.9	-2.26
0.9	1.67332		1.71778		-2.59
1.0	1.732051	1.826949	1.784771	-9.5	-2.95

Example 2

Use a) the midpoint, and b) the fourth–order Adams methods to solve problem (Example 1) with h = 0.1.

Solution. a)The first step in the midpoint method is to compute

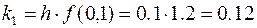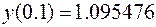. The second step is to compute . Therefore, . The computation is repeated, and the results are summarized in Table 5.4.

b)A popular multistep method based on the Adams integration formulas uses the fourth-order Adams-Bashforth formula as the predictor and the fourth-order Adams-Moulton formula as the corrector (see Table 5.2). Because Adams’s methods are not self-starting, we depend upon one step method (midpoint) to get the four initial slopes 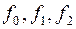and 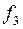(see Table 5.4).

TABLE 5.4.

x	y_true	y_midpoint	y_Adams	f_i	e_t, %
midpoint	Adams
	1.0	1.0		1.0
0.1	1.095445	1.095476		0.912907	-0.003
0.2	1.183216	1.183298		0.84526	-0.007
0.3	1.264911	1.265057		0.79077	-0.012
0.4	1.341641	1.34186	1.341809	0.745599	-0.016	-0.013
0.5	1.414214	1.414516	1.414407	0.707398	-0.021	-0.014
0.6	1.48324	1.483638	1.483465	0.674549	-0.027	-0.015
0.7	1.549193	1.549702	1.549457	0.645915	-0.033	-0.017
0.8	1.612452	1.613088	1.612761	0.620674	-0.039	-0.019
0.9	1.67332	1.674106	1.673684	0.598213	-0.047	-0.022
1.0	1.732051	1.733012	1.732481	0.578066	-0.056	-0.025

Problems

1. Solve the following initial-value problem analytically over the interval from 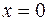to 1: 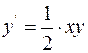where 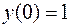. Plot the solution.

2. Use the a) Euler, and b) midpoint methods with 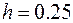to solve Prob. 1. Plot the results on the same graph to visually compare the accuracy for the two numerical methods.

3. Solve the following initial-value problem from to 5: 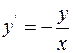. Use a step size of 0.5 and initial value of 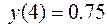. Obtain your solutions using the following techniques: a) the fourth-order RK method, and b) the fourth-order Adams method. Compare and discuss the results.

Date: 2016-01-14; view: 776

<== previous page	\|	next page ==>
For finding roots of algebraic and transcendental equations	\|	Part 6. Interpolation and Extrapolation of Functions

doclecture.net - lectures - 2014-2024 year. Copyright infringement or personal data (0.007 sec.)