
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Part 3. Solution of Linear Algebraic Equations
TABLE 3.1 Comparison of the characteristics of alternative methods
| Method | Stability | Precision | Breadth of Application |
| Cramer's rule | — | Affected by round-off error | Limited |
| Gaussian Elimination with Back Substitution | — | Affected by round-off error | General |
| Jacobi Iteration | May not converge if not diagonally dominant | Excellent | Appropriate only for diagonally dominant system |
| Gauss - Siedel Iteration | May not converge if not diagonally dominant | Excellent | Appropriate only for diagonally dominant system |
TABLE 3.2 Summary of important information
| Method | Procedure | Potential problems and remedies |
| Gaussian Elimination with Back Substitution | 
| Problems: Ill conditioning Round – off Division by zero Remedies: Higher precision Partial pivoting |
| Compute Determinant with Gaussian Elimination | 
| Problems: Ill conditioning Round – off Division by zero Remedies: Higher precision Partial pivoting |
| Jacobi Iteration |  ; ;  ; ;  , ,  , ,  ; ;  ;continue iteratively until ;continue iteratively until 
| Problems: Divergent or convergent slowly Remedies: Diagonal dominance Relaxation |
| Gauss -Seidel Iteration |  ; ;  ; ;  , ,  , ,  ; ;  ; continue iteratively until ; continue iteratively until 
| Problems: Divergent or convergent slowly Remedies: Diagonal dominance Relaxation |
Example 1
Suppose we want to solve the linear system:
 (1)
(1)
with (a)Gaussian Elimination with Back Substitution, (b)Gauss - Seidel Iteration, (c)Check your results by substituting them back into the original equations (1). Carry five significant figures during the computation.
Solution.
(a)Gaussian Elimination with Back Substitution:
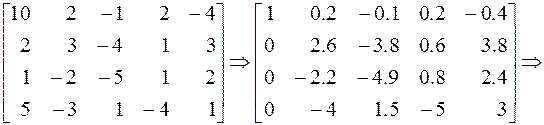


After these operations we can solve this linear system of equations (1) by back substitution:

This solution can be verified by substituting the results into the original equation set (1):




(b)Gauss - Seidel Iteration;
First, solve each of the equations (1) for its unknown on the diagonal.

Suppose we choose the initial approximation as:

The first approximate solution is given by (Tab. 3.2):




The second approximate solution is given by substituting the calculated values:




For this case the method is slow converging (or diverging) on the true solution. Let us choose the initial approximation as solution (a) of linear system (1) with two significant figures:

The first approximate solution is given:

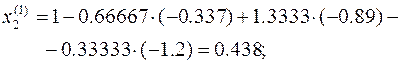


Convergence can be checked using the criterion:

Consequently, provide a means to estimate the error:
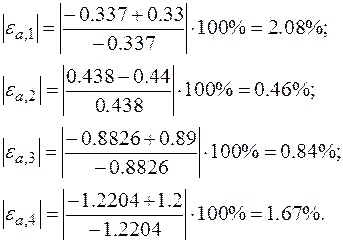
Because  is not less than the required value of
is not less than the required value of  , we would continue to compute a set of new x's:
, we would continue to compute a set of new x's:



Now the error estimates are:

 and
and  .
.
Example 2
Consider the linear system:

Use Gauss-Jordan elimination to solve this system.
Solution. First, express the coefficients and the right - hand side as an augmented matrix:

Then, normalize the first row by dividing it by the pivot element 3, to yield:

The  term can be eliminated from the second row by subtracting -2 times the first row from the second row. Similarly, subtracting 2 times the first row from the third row will eliminate the
term can be eliminated from the second row by subtracting -2 times the first row from the second row. Similarly, subtracting 2 times the first row from the third row will eliminate the  term from the third row:
term from the third row:

Next, normalize the second row by dividing it by 0.33334:

Reduction of the  terms from the first and third equations gives:
terms from the first and third equations gives:

The third row is then normalized by dividing it by 3.0000:

Finally, the  terms can be reduced from the first and the second equations to give
terms can be reduced from the first and the second equations to give

Thus, the coefficient matrix has been transformed to the identity matrix, and the solution is obtained in the right-hand-side vector.
Notice that no back substitution was required to obtain the solution by the Gauss-Jordan technique.
Problems
1. For the set of equations:

a)Use the Cramer's rule to solve for the x's.
b)Compute the determinant using Gaussian elimination with back substitution.
c)Substitute your results back into the original equations to verify your solution.
2. Determine the inverse matrix using Gaussian elimination with back substitution:
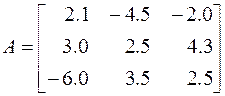 .
.
Multiply the inverse by the original coefficient matrix and assess whether the result is close to the identity matrix.
3. Given the linear system of equations:

Solve it with: a)Gauss-Jordan method, b)Jacobi iteration, c)Gauss - Seidel iteration.Forb)andc)provide a means to estimate the error.
Date: 2016-01-14; view: 1336
| <== previous page | | | next page ==> |
| Part 2. Numerical Integration | | | For finding roots of algebraic and transcendental equations |