
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Volba spotřebitele v ordinalistické teorii
1. Které z následujících tvrzení platí pro dvě kombinace dvou statků spotřebního koše, které leží na téže křivce indiference?
a. celkový užitek z obou kombinací je stejný
b. mezní užitek z obou kombinací je stejný
c. kombinaci ležící více vlevo nahoře preferuje spotřebitel více
d. spotřebitel hodnotí obě kombinace stejně
2. Směrem zleva doprava na křivce indiference:
a. Roste celkový užitek
b. dochází ke změně mezní míry substituce
c. klesá celkový užitek
d. dochází ke změně poměru mezních užitků
3. Křivka indiference vyjadřuje:
a. preference spotřebitele
b. omezení spotřebitele důchodem
c. stejný celkový užitek spotřebitele
d. rozpočtové možnosti spotřebitele
4. Axiom tranzitivity se na grafu křivek indiference projevuje:
a. Jejich konvexním tvarem
b. tím, že se křivky indiference neprotínají
c. tím, že křivky indiference protínají obě osy
5. Zákon poklesu mezního užitku se v modelu křivek indiference projevuje:
a. tím, že křivky indiference mají konvexní tvar
6. Jestliže kombinace A leží na výše položené křivce indiference než kombinace B, platí, že:
a. Spotřebitel preferuje obě kombinace stejně
b. spotřebitel preferuje A před B
c. spotřebitel preferuje B před A
7. Komplementární vztah dvou statků se v modelu křivek indiference projevuje:
a. Tím, že křivky indiference neprotínají
b. tím, že se křivky indiference nedotýkají os
8. Substituční vztah dvou statků se v modelu křivek indiference projevuje:
a. tím, že křivky indiference protínají dvě osy
b. tím, že křivky indiference mají konverxní tvar
9. Vztah, při kterém je jeden ze dvou statků nezbytný a druhý luxusní, se v modelu křivek índiference projevuje:
a. tím, že křivky indiference protínají jednu osu
b. tím, že křivky indiference jsou lineární
10. Mezní míra substituce:
a. je vždy rovna v absolutní hodnotě podílu mezních užitků obou statků
b. je vyjádřena sklonem křivky indiference
11. Má-li funkce celkového užitku spotřebitele ze dvou statků q1, q2 následující podobu TU = aq1 + bq2 + q1q2, za podmínek a > 0, b > 0, platí, že:
a. křivky indiference protínají obě osy
b. oba statky jsou substituty
12. Má-li funkce celkového užitku spotřebitele ze dvou statků q1, q2 následující podobu TU = aq1 + bq2 + q1q2, za podmínek a > 0, b < 0, platí, že:
a. křivky indiference protínají jednu osu
b. oba statky jsou nepřímé substituty (q1 nezbytný, q2 zbytný)
13. Má-li funkce celkového užitku spotřebitele ze dvou statků q1, q2 následující podobu TU = aq1 + bq2 + q1q2, za podmínek a < 0, b < 0, platí, že:
a. oba statky jsou komplementy
b.  křivky indiference se nedotýkají os
křivky indiference se nedotýkají os
14. Má-li funkce celkového užitku spotřebitele dvou statků , c > 0, d > 0, c+ d = 1, platí, že:
a. křivky indiference neprotínají osy
b. oba statky jsou nezávislé
15. Spotřebitelem zvolená kombinace množství dvou statků je charakterizována vztahem  a je rozpočtově dostupná. Platí, že:
a je rozpočtově dostupná. Platí, že:
a. má-li být spotřebitel v bodě optima, množství q1 se musí snížit a množství q2 zvýšit
16. Spotřebitel spotřebovává 2 statky. Uvažuje o zařazení třetího. Za které podmínky, vyjádřené následujícími vztahy, spotřebitel 3. statek do spotřebního koše zařadí:
a. 
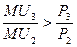 je správně
je správně
17. Spotřebitel užívá přímé substituty, je-li funkce jeho celkového užitku:
a. TU = aq1 + bq2 + q1q2, kde platí a > 0, b > 0, TU > 0
18. Je-li funkce celkového užitku spotřebitele TU = aq1 + bq2 + q1q2, kde platí a > 0, b > 0, TU > 0, a zvýší se důchod spotřebitele, platí, že v bodě optima:
a. Mezní míra substituce se zvýší
b. mezní míra substituce se nezmění
c.  mezní míra substituce se sníží
mezní míra substituce se sníží
19. Je-li funkce celkového užitku spotřebitele dvou statků , po zvýšení ceny prvního statku P1 (uvažujeme efekt metody statického rozkladu) při optimální kombinaci:
a. dochází jen k substitučnímu efektu na q1
b. dochází jen k důchodovému efektu na q1
c. se sníží obě spotřebovávaná množství q1,q2
d. se sníží jen q2
e. se sníží jen q1
20. Jestliže se v případě spotřebitele s funkcí celkového užitku ad) 4 zvýší ceny obou statků stejným tempem (o 20%):
a. klesne spotřebované množství obou statků
b. projeví se jen důchodový efekt (podle metody statického rozkladu)
c. projeví se oba efekty
d. změní se jen q1, na q2 to nemá vliv
e. množství obou statků klesne vždy ve stejném poměru
21.  Je li funkce celkového užitku spotřebitele dvou statků , spotřebitel vydává na první statek výdaje ve výši:
Je li funkce celkového užitku spotřebitele dvou statků , spotřebitel vydává na první statek výdaje ve výši:
a. c/(c+d) svého důchodu
22. Je-li funkce celkového užitku spotřebitele TU = aq1 + bq2 + q1q2, kde platí a > 0, b < 0, TU > 0, potom platí, že:
a. může nastat situace, kdy spotřebitel kupuje pouze statek q2
b. může nastat situace, kdy spotřebitel kupuje pouze statek q1
c. spotřebitel vždycky kupuje určité množství obou statků
23. Je-li funkce celkového užitku spotřebitele TU = aq1 + bq2 + q1q2, kde platí a < 0, b < 0, TU > 0, potom platí, že:
a. oba statky jsou oboustranně zastupitelné
b. může nastat situace, kdy spotřebitel kupuje pouze statek q1
c. může nastat situace, kdy spotřebitel kupuje pouze statek q2
d. spotřebitel vždycky kupuje určité množství obou statků
24. Je-li funkce celkového užitku spotřebitele TU = aq1 + bq2 + q1q2, kde platí a < 0, b > 0, TU > 0, potom platí, že:
a. může nastat situace, kdy spotřebitel kupuje pouze statek q1
b. může nastat situace, kdy spotřebitel kupuje pouze statek q2
c. spotřebitel vždycky kupuje určité množství obou statků
d. oba statky jsou oboustranně zastupitelné
25. Je-li funkce celkového užitku spotřebitele TU = aq1 + bq2 + q1q2, kde platí a > 0, b > 0, TU > 0, potom platí, že:
a. Může nastat situace, kdy spotřebitel kupuje pouze statek q1
b. Může nastat situace, kdy spotřebitel kupuje pouze statek q2
c. oba statky jsou oboustranně zastupitelné
d. spotřebitel vždycky kupuje určité množství obou statků
8 Firma jako tržní subjekt
1. Firmy působí:
a. Na trhu výrobních faktorů
b. Na trhu statků a služeb
c. Na žádném z těchto trhů
d. na obou těchto trzích (výrobních faktorů a statků & služeb)
2. Firma na trhu statků služeb vystupuje vždy:
a. na straně nabídky
3. Jestliže firma dosahuje záporného ekonomického zisku, pak účetní zisk:
a. nelze jednoznačně určit (zda je kladný, nebo záporný)
4. Jestliže firma dosahuje ekonomický zisk, pak účetní zisk:
a. musí být také kladný
5. Zaškrtněte, kdy se zvýší účetní zisk firmy:
a. jestliže se zvýší ceny výrobních faktorů
b. jestliže se zvýší ceny vyráběných produktů
c. sníží se ceny energií
6. Účetní (bilanční) zisk firmy vyjadřujeme jako:
a. ekonomický zisk + implicitní náklady
b. příjmy - explicitní náklady
7. Krátké období je charakterizováno:
a. firmy nemohou rozšiřovat svoje výrobní kapacity
b. alespoň jeden výrobní faktor zůstává fixní
8. Pro velmi dlouhé období platí:
a. Jde vždy o období nad 5 let
b. všechny používané vstupy jsou variabilní
c. dochází ke kvalitativním změnám v technické úrovni
9 Produkční funkce firmy
1. Jaká je nejdůležitější vlastnost produkční funkce v krátkém období?
a. v krátkém období existuje více variabilních faktorů
b. v krátkém období existuje pouze jeden variabilní faktor
c. nejdůležitější vlastnosti produkční funkce je technický název pro vztah mezi minimálním množstvím výstupu a požadovanými vstupy
d. zákon klesajících výnosů platí vždy v dlouhém období
2. Určete. které tvrzení je správné pro degresivní produkční funkci:
a. Konstantní průměrné a mezní produkty faktorů
b. Rostoucí průměrné a mezní produkty faktorů
c. klesající průměrné faktory
d. až do určitého množství faktorů rostoucí a po překročení tohoto množství klesající průměrné a mezní produkty
3. Který z výroků je správný? Progresivně degresivní produkční funkce má v inflexním bodu:
a. maximum mezního produktu
4. Produkční funkce předpokládá:
a. Stále ceny dovozu
b. neměnnou technologii
c. dokonalou konkurenci na trzích výrobních faktorů
d. změny úrovně outputu při stejné úrovni inputu
5. Izokvanta vyjadřuje:
a. kombinaci výrobních faktorů, jejichž pomocí je možno vyrobit různý objem produkce
b. kombinaci výrobních faktorů, jejichž pomocí je možno vyrobit stejný objem produkce
c. náklady vynaložené na nákup technologie
d. žádná z nabízených možností není správná
6. Mezní produkt je:
a. změna objemu vyrobené produkce vyvolané změnou množství inputu o jednotku
7. Izokosta (linie celkových - stejných nákladů) vyjadřuje:
a. maximálně dostupné kombinace inputů v rámci daných celkových nákladů
8. Který vztah vyjadřuje klesající výnosy variabilního vstupu:
a. Q = ÖL
9. Produkční funkce jsou dány následujícími vztahy, rozhodněte, v kterém případě jde o rostoucí výnosy z rozsahu:
a. Q = K * L
10. Který vztah vyjadřuje v dlouhém období situaci vstupů, tj. mezní míru technické substituce (MRTS):
a. vyjadřuje míru, v níž je možné nahradit jeden výrobní faktor výrobním faktorem druhým při konstantním výstupu
b. vyjadřuje, jaké množství jednoho faktoru se může zvýšit při konstantním množství druhého faktoru
c. poměr, v jakém dva výrobní faktory za sebe nahradit, pokud produkce poroste
d. neplatí žádná z variant
10 Nákladové funkce firmy
1. Z následujících příkladů nákladů firmy určete, které se mění s množstvím produktu:
a. pracovní (mzdové) náklady
b. peněžní výdaje na suroviny při konstantních cenách surovin
c. úrok z investičního úvěru
d. daň z nemovitosti
2. Je nutné v ekonomických analýzách rozlišovat:
a. průměrný variabilní a průměrný fixní náklad? - ANO
b. mezní variabilní a mezní celkový náklad? -NE
3. Křivka mezních nákladů:
a. žádná odpověď není správná
4. Křivka mezních nákladů ve tvaru U:
a. protíná křivku AVC vždy v jejím minimu
5. V krátkém období s růstem produkce:
a. Průměrné fixní náklady jsou vždy konstantní
b. průměrné fixní náklady klesají vždy
c. Průměrné fixní náklady rostou
6. Jestliže produkční funkce v krátkém období vykazuje rostoucí výnosy z variabilního vstupu:
a. variabilní náklady rostou
b. průměrné náklady klesají
7. Jestliže produkční funkce v krátkém období vykazuje klesající výnosy z variabilního vstupu:
a. variabilní náklady rostou
b. průměrné variabilní náklady rostou
8. V dlouhém období:
a. všechny vstupy jsou variabilní
9. Jestliže produkční funkce v krátkém období vykazuje rostoucí výnosy z variabilního vstupu:
a. variabilní náklady rostou
10. Jestliže v určitém intervalu funkce celkových nákladů rostou náklady rychleji než roste množství produkce, pak v tomto intervalu:
a. průměrný náklad roste
b. mezní náklad roste
11. Vztah mezi dlouhodobými a krátkodobými náklady:
a. STC jsou zpravidla vyšší než LTC ( STC – krátké celkové náklady, LTC – dlouhé celkové náklady
12. Křivka mezních nákladů protíná:
a. křivku průměrných nákladů vždy v jejím minimu
b. křivku průměrných variabilních nákladů vždy v jejím minimu
13. Účetní (bilanční) zisk firmy vyjadřujeme jako:
a. ekonomický zisk + implicitní náklady
b. příjmy - explicitní náklady
14. Nebude-li firma v krátkém období vyrábět:
a. variabilní náklady budou záporné
b. variabilní náklady budou nulové
c. variabilní náklady budou kladné
15. Nebude-li firma v krátkém období vyrábět:
a. fixní náklady budou kladné
16. Nebude-li firma v dlouhém období vyrábět:
a. fixní náklady budou nulové
17. Izokosta vyjadřuje:
a. kombinaci vstupů v rámci celkových nákladů
18. Průměrné variabilní náklady firmy se v krátkém období rovnají mezním nákladům. Co doporučíte firmě, měla by:
a. zvýšit produkci zásob
b. produkci stabilizovat či snad
c. snížit, ( z hlediska optimalizace(minimalizace) průměrných celkových nákladů )
19. Průměrné náklady firmy jsou v krátkém období nižší než mezní náklady. S rozšiřováním produkce budou průměrné náklady:
a. Stoupat
11.1 Charakteristika dokonalé konkurence a utváření nabídky firmy v krátkém období
1. Předpokládejme, že dokonale konkurenční odvětví je tvořeno 4 firmami s následujícími nabídkovými funkcemi. Jaká bude tržní nabídka tohoto odvětví? Q 1=8+2P , Q2=5+5P, Q3=16+4P, Q4=10+5P:
a. Q=39 + 16P
2. V čem spočívá výrobní efektivnost dokonale konkurenčního trhu:
a. Firmy vyrábějící takový výstup, který spotřebitelé požadují
b. ve skutečnosti, že výstup je vyráběn s minimální na jednotku produkce každá, z firem vyrábí výstup s minimálními průměrnými náklady
c. ve skutečnosti, že výstup je vyráběn s minimální na jednotku produkce každá, z firem vyrábí výstup s maximálními průměrnými náklady
d. firmy v dokonalé konkurenci nemohou zvětšit výstup pouhým přerozdělením vstupů
3. Křivka krátkodobé nabídky firmy v dokonale konkurenční firmě je tvořena:
a. rostoucí částí křivky mezních nákladů, jejíž spodní hranicí je minimum AC
4. Základním rysem dokonalé konkurence je:
a. Možnost tržních subjektů ovlivnit tržní cenu
b. nemožnost tržních subjektů ovlivnit tržní cenu
c. cena se v podmínkách dokonalé konkurenci rovná celkovým příjmům
d. v bodě optima platí, že P > MC
5. Kdy funkce zisku v dokonale konkurenční firmě nabývá svého maxima, za jakého předpokladu:
a. P = MC
6. Firma v krátkém období nechává činnost, jestliže:
a. celkové příjmy budou nižší než variabilní náklady
11.2 Dlouhé období a utváření tržní nabídky v dokonalé konkurenci
1. Dokonalá konkurence je v dlouhém období charakterizována:
a. Kladným ekonomickým ziskem
b. Vstupem nových firem do odvětví, za předpokladu, že v krátkém období je v odvětví dosahován ekonomický zisk
c. vztahem rovnosti ceny produkce a minimálních průměrných nákladů jako podmínky rovnováhy firmy
d. firmy realizují pouze normální zisk
2. Který z následujících vztahů vyjadřuje tendenci v dokonale konkurenčním odvětví v dlouhém období:
a. Min AC = MC
b. P = AC
c. AR = MR = P
d. AR = MC
e. P=MC=min AC
13 Monopol (jediný prodávající) - nabídka firmy
1. V podmínkách nedokonalé konkurence a tedy i monopolu platí, že s růstem výroby:
a. mezní příjem je nižší než cena
2. Optimální výstup produkce dosahuje monopol zpravidla, jsou-li průměrné náklady:
a. nemusí být minimální
3. Je-li nabídka produktu v daném odvětví zajišťována jedinou firmou, pak se situací dokonale konkurenční platí (předpokládáme stejné funkce poptávky a stejné funkce nákladů):
a. nabízené množství je nižší a cena vyšší
b. nabízené množství je vyšší a cena nižší
c. nabízené množství je nižší a cena nižší
d. nabízené množství je vyšší a cena vyšší
4. Chce-li podnik maximalizovat zisk:
a. musí se rovnat mezní příjem mezním nákladům
5. Křivka poptávky po produkci monopolu je:
a. je totožná s křivkou poptávky
6. Při analýze produkce monopolu bylo zjištěno, že mezní příjmy jsou 11 Kč a mezní náklady pak 10 Kč. Co byste doporučil udělat, aby zisk monopolu byl maximální:
a. Zvýšit ceny
b. Zvýšit ceny a snížit produkci
c. Snížit ceny
d. snížit ceny a zvýšit produkci
e. ponechat ceny i produkci stejné
14 Monopolistická konkurence - nabídky firmy
1. Který z následujících vztahů je podmínkou rovnováhy monopolistické firmy maximalizující zisk v krátkém období:
a. MR=MC
2. Dlouhodobá rovnováha monopolistická konkurence se ustálí v bodě, kde:
a. křivka individuální poptávky je tečnou křivky AC
3. Důležitým znakem monopolistické konkurence je, že dlouhodobý rovnovážný výstup firmy se nachází na úrovni výstupu:
a. nižším než výstup, při němž jsou AC minimální
4. Určete, kdy je firma výrobně efektivní:
a. Platí podmínka vyrovnání mezních nákladů s prostředky, které jsou kupující ochotni vydat na koupi dodatečné jednotky produkce
b. trh nutí výrobce k tomu, aby vyráběli rozsah produkce, při kterém jsou minimalizovány náklady na jednotku produkce
c. platí následující rovnost MU=MC
d. jde o část přebytků, které vznikají v důsledku omezení rozsahu produkce
5. Jaký bude mít ekonomický zisk monopolistická konkurenční firma v dlouhém období:
a. nulový
6. Monopolistická konkurence je struktura trhu, pro kterou neplatí:
a. zboží je homogenní
b. relativně volný vstup a výstup do odvětví, existují pouze malé a snadno překonatelné překážky
c. cíl firmy – maximalizace zisku
d. velký počet firem, žádná není tak silná, aby mohla ovlivnit tržní cenu P
7. V jakém vztahu v monopolistické konkurenční firmě jsou cena a mezní náklady:
a. P > MC
8. Firma maximalizuje tržby. Její optimum leží v bodě, kde:
a. MR = 0
9. Klesající mezní příjem firmy je neslučitelný s:
a. dokonalou konkurencí
10. Individuální poptávková křivka bude lineární na nedokonale konkurenčním trhu. V bodě, kde TR jsou maximální, MR musí být:
a. nulový
15 Oligopolní konkurence
1. V oligolním odvětví vyrábějí vždy všechny firmy heterogenní produkt.
a. ne
2. V modelu oligopolu s dominantní firmou se předpokládá, že poptávka po produkci dominantní firmy je ve srovnání s tržní poptávkou elastičtější.
a. ano
3. Musí být kartel vždy úspěšný? Vysvětlete, proč kartelové dohody nejsou dlouhodobě stabilní.
a. Ne
4. Stackelbergův model stanoví, že je pro firmu výhodné má-li možnost stanovit množství produkce dříve než zjistí, kolik vyrábí její rival.
a. Ano
5. Sweezyho model oligopolu (se zalomenou křivkou poptávky) vysvětluje, proč každá firma ponechává svou cenu bez ohledu na chování konkurentů.
a. ne
6. Sweezyho model neumožňuje určit cenu, protože je mezera mezi křivkami MR a MC.
a. Ne
7. Sweezyho model vysvětluje rigiditu ceny, ale nevysvětluje její určení.
a. Ano
8. Sweezyho model oligopolu předpokládá, že poptávka po produkci firmy je méně elastická pokud firma cenu sníží než když cenu zvýší.
a. Ano
"V bode nasycení"
je celkový užitek maximální."
je mezní užitek nulový."
"Které z následujících tvrzení platí pro dvě kombinace dvou statku spotřebního koše, které leží na téže křivce indiference"
celkový užitek z obou kombinací je stejný"
spotřebitel hodnotí obě kombinace stejně"
Komplementární vztah dvou statku se v modelu křivek indiference projevuje"
tím, že se křivky indiference nedotýkají os."
Jestliže v určitém intervalu funkce celkových nákladu rostou náklady pomaleji než množství produkce, pak v tomto intervalu"
mezní náklady jsou vyšší než průměrné"
je nákladová funkce degresivní"
Vztah, při kterém je jeden ze dvou statku nezbytný a druhý luxusní se v modelu křivek indiference projevuje"
tím, že křivky indiference protínají jednu osu"
V rámci ordinalistické verze teorie užitku popište způsob řešení tohoto problému:“
ceny statku, množství statku a výši spotřebitelova důchodu"
Optimum spotřebitele nastává, když je splněna tato podmínka"
MU1/MU2 = P1/P2
Y = P1q1 + P2q2
MPL v krátkém období je větší než APL. Jaké budou při tomto předpokladu MC vporovnání s AVC?"
menší"
Podmínkou maximalizace zisku firmy je"
MR = MC
Statky káva a mléko k sobě mají vztah jako"
komplementy
Zvýšení úrokové míry je výhodnější pro"
"věřitele"
"střadatele"
Mezi alternativní cíle firmy nepatří"
maximalizace objemu produkce
maximalizace dividendy na akcii
maximalizace zisku
minimalizace nákladu"
Pokud změna ceny statku A nevyvolá žádnou změnu v poptávce po statku B, potommůžeme říci, že:"
Oba statky A a B se řadí mezi inferiorní zboží
Pokud růst ceny statku A vyvolá posun poptávkové křivky po statku B doleva, potommůžeme říci, že:"
Statky A a B jsou komplementy
Pokud klesne cena dřeva, z kterého je vyráběn nábytek, potom přebytek spotřebitelů nábytku"
Vzroste
Víme, že daný spotřebitel je vždycky ochoten vyměnit 2 pomeranče za jeden grapefruit. Pokud budeme na horizontální ose vynášet množství spotřebovaných pomerančů ana vertikální množství spotřebovaných grapefruitu, potom indiferentní křivka daného spotřebitele bude"
Přímka se sklonem -1/2"
Přímka se sklonem +1/2
Přímka se sklonem +2"
Konvexní směrem k počátku
Koncové body (průsečíky s osami) rozpočtové křivky"
Vyjadřují sklon rozpočtové křivky"
Představují nejvyšší možné množství daných statků, které si spotřebitel může koupit, pokud celý svůj důchod utratí za dané zboží"
Pokud víme, že ceny dvou statků se rovnají (PA = PB), potom pokud spotřebitel bude maximalizovat svůj užitek"
Mezní užitek statku A (MUA) musí být roven meznímu užitku statku B (MUB)"
Víme, že v bodě rovnováhy je cenová elasticita poptávky -1,2 a cenová elasticita nabídky +0,6. Pokud vládou určená cena bude o deset procent nižší než rovnovážná cena, potom"
Nastane na trhu přebytek zboží ve výši 1,8 % rovnovážného množství"
Nastane na trh přebytek ve výši 12 % rovnovážného množství"
Na trhu nastane nedostatek zboží ve výši 18% rovnovážného množství
Na trhu nastane nedostatek ve výši 6 % rovnovážného množství"
Pokud víme, že průměrný produkt 6 pracovníka je 15 a mezní produkt 7 pracovníka je 18, potom můžeme říci, že:"
Se nacházíme na rostoucí části křivky průměrného produktu
Pokud se pohybujeme po izokvantě z leva doprava (předpokládáme konvexní tvar), potom platí, že:"
Dochází k současnému růstu mezního produktu jednoho výrobního a poklesu mezního produktu faktoru druhého "
Vyberte správné tvrzení:"
Podle ordinalistické teorie užitku, nelze odvodit individuální poptávku spotřebitele po statku, protože dle této nelze užitek přesně změřit"
Cenová elasticita poptávky se pohybuje vždy v intervalu od nuly do nekonečna."
V dlouhém období mohou nové firmy vstupovat do odvětví, mohou měnit všechny výrobní faktory i svou velikost firmy ale nemohou měnit produkční technologie."
Průměrné fixní náklady firmy jsou vždycky klesající
Předpokládáme, že spotřebitel kupuje pouze dva statky. Pokud se sníží cena jednoho
z nich, povede to:"
K růstu mezní míry substituce"
Ke změně sklonu rozpočtové křivky
Ke změně tvaru indiferenční křivky"
Ke růstu mezního užitku toho statku, jehož cena se nezměnila.
Které z následujících tvrzení je pravdivé?"
Cenová elasticita poptávky je vždy kladná"
Inferiorní zboží je takové jehož důchodová elasticita je kladná"
Giffenuv statek je takový statek, který nemá žádné přímé substituty"
Luxusní zboží je takové zboží, jehož důchodová elasticita je v absolutní hodnotě větší než jedna
Pokud spotřebitel maximalizuje svůj užitek ze dvou statku (X,Y), potom v bode optima platí:"
Px/Py se rovná poměru výdajů na oba statky"
Py/Px| = |MRSx/y|"
Ze sklonu indiferenční křivky:"
Můžeme určit poměr v jakém je spotřebitel ochoten vyměňovat jeden statek za druhý"
"Můžeme odvodit relativní ceny obou statků"
Křivka, která reprezentuje všechny kombinace poskytující stejnou úroveň užitku se nazývá"
Indiferenenční křivka"
Monika maximalizuje svůj užitek ze spotřeby výběrem spotřebního koše, v němž poměry mezních užitků a cen jednotlivých statků jsou shodné pro všechny statky. Přesto existuje statek, který, ačkoliv je pro Moniku dostupný, není v jejím spotřebním koši zastoupen. Je tomu tak proto, že poměr mezního užitku tohoto statku a ceny tohoto statku je:"
"Příliš nízký"
Pokud vláda reguluje ceny tak, že tržní cena je pod rovnovážnou úrovní"
"Někteří spotřebitelé těží z cenové regulace, zatímco jiní jsou na tom v důsledku cenové regulace hůře
Předpokládejme, že pivo a víno jsou substituty. Pokud cena piva vzroste"
"Křivka poptávky po víně se posune doprava"
Která z následujících změn nejpravděpodobněji způsobí posun poptávky po skriptechdoprava"
"Snížení ceny skript"
"Zvýšení studentských stipendií
Funkce Tu=8g1+2g2+g1+g2, důchod Y=22, P1=3, P2=1. P1 se změní na P1=2. Určete substituční efekt změny ceny P1 na Q1.
4)  Q1SE = 2/3,
Q1SE = 2/3,  Q2SE =-1
Q2SE =-1
V kardinalistické verzi teorie užitku určete optimální množství spotřebních statků, pokud víte, že Tu=24Q – 3Q2
Pokud je důchodová spotřební křivka rostoucí v celém svém oboru, pak můžeme říct, že:
oba statky pro které byla křivka odvozena, jsou normální
pouze statek, který je na horizontální ose, je normální
pouze statek, který je na vertikální ose, je normální
ostatní statky jsou inferiorní (?)
Date: 2016-01-03; view: 2301
| <== previous page | | | next page ==> |
| Tržní rovnováha na trhu jednoho statku | | | Trh práce, kapitálu a půdy |