
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Laboratory work ¹ 42
MATHEMATICAL PENDULUM
Purpose of work: to measure the free fall acceleration.
INSTRUMENTATION AND APPLIANCES: mathematical pendulum; the stop-watch, straightedge.
Short theory
The point mass suspended by means of an unelastic weightless thread is called the mathematical pendulum. The restoring force is the projection of the force of gravity P=mg on the direction of motion of the point mass. In this case
 ,
,
where a = x/l, the angle between positions of l in free state and deviation state.
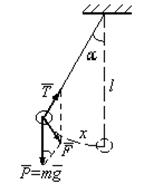
Figure 4.1
If the angles a are so small that sina » a, then
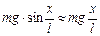 .
.
Since this force is always directed to the equilibrium position and that is why it has a sign opposite to that of x:

In this case the oscillations are harmonic. The second Newton’s law is
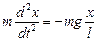 .
.
Finally we obtain the differential equation of harmonic oscillations:
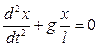 .
.
If g/l=w2, then
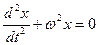 .
.
Solution of this equation is

The cyclic frequency is
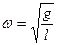 ,
,
and period is equal
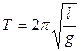 ,
,
i. e., the frequency and the period of oscillations do not depend on the mass of the oscillating body; they are determined only by the length of the thread and the free fall acceleration. The measurement of the period of a mathematical pendulum is used for determine g:
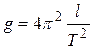 .
.
Experimental part
1. Fix the end of the cord in the first position (l = 50 cm). Make the pendulum vibrate (the amplitude of vibration must not be more than the ball diameter). Determine time of 50 oscillations by the stop-watch three times and calculate the period T using the average value of the time.
2. Determine the free fall acceleration g.
3. Calculate an error.
4. Investigate relation between the period T and the length l. Put the end of the cord in the second position (l = 150 cm). Calculate period of oscillations 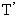 in the same way and compare with T.
in the same way and compare with T.
5. Increase the amplitude of oscillations twice. Test independence of the period on the amplitude of oscillations (small amplitude and big amplitude).
6. Make conclusions.
Control questions
1. What is a mathematical pendulum?
2. What kind of oscillations is called harmonic?
3. Write the differential equation of harmonic oscillations.
4. Write the dependence of deviation upon time for harmonic oscillations. Show this dependence in figure.
5. Give definitions for a period, an amplitude, a frequency, a cyclic frequency and a phase of vibration.
Authors: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol ¹ 6 from 30.03.2009 .
Date: 2015-12-24; view: 1174
| <== previous page | | | next page ==> |
| From (2.5) and (2.6) get the period of oscillation of the spring pendulum | | | LABORATORY WORK ¹ 43.2 |