LABORATORY WORK № 43.2

OSCILLATION OF PEG

Purpose of work is to probe dependence of period of oscillations of peg on distance between the axis of rotation and center of peg.

Devices: peg, straightedge, stop-watch.

Task of work: 1) to build the theoretical and experimental graph of dependence of period of oscillations T of peg from dimensionless length : ;

2) to find minimum functions by an experimental and theoretical way.

Theoretical part

Will consider oscillation of peg, position of axis of which, it is possible to change along a peg. Such peg shows by itself a physical pendulum. The period of oscillation of the physical pendulum is determined by formula

, (8.1)

Where I is a moment of inertia of peg, m is mass, a is distance from the axis of rotation to the center of the masses, g is the free fall acceleration. The moment of inertia I in this case is determined on the theorem of Steiner:

, (8.2)

where I₀ is a moment of inertia of peg in relation to an axis which go athwart to the peg through his center:

(8.3)

After a substitution (8.2) and (8.3) in a formula (8.1) get:

(8.4)

In the formula (8.4) the size a can change in the interval: .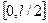

1. At , period , that at fixing of peg in a center of peg it will not oscillate in general, in this case the total moment of forces which operate on a peg in any its position will equal a zero.

2. At for T get:

(8.5).

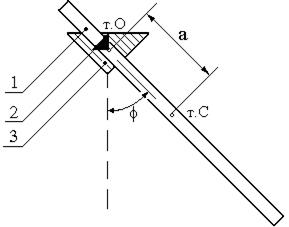
Figure 8.1

3. Research of formula (8.4) shows on the extremum, that a function has minimum, a coordinate of which is from a condition . After differentiation (8.4) find, that a function has minimum at

, (8.6)

or approximately at .

For experimental research of dependence of period of oscillations of peg from position of axis of rotation a device, represented on fig. 8.1, is used. If peg 1 to set a supporting prism 2 on a bracket 3, to show out of position of equilibrium on some corner and to release, then he will carry out oscillation in relation to position of equilibrium.

Practical part

1. Measure length of peg - l.

2. Set a supporting prism 2 on the first value from a table.

3. Set a peg on a bracket 3.

4. Show a pendulum out of position of equilibrium on a corner and to release; to measure time 10 full oscillations. Write down the period of T to the table 8.1.

5. Repeat measurings with other the values a which are indicated in a table 8.1.

Table 8.1

n	/l	, cm	T, s	l, cm
experiment	theory
	0,01
	0,02
	0,03
	0,04
	0,05
	0,1
	0,2
	0,3
	0,4
	0,45

6. After a formula (8.4) to expect the theoretical values of period of T. To compare the experimental and theoretical values of period.

7. On one field (it is desirable on a plotting paper) to build theoretical and experimental graph according to sample, which is presented on fig. 8.2.

8. Find the first derivative of function (8.4) on a parameter . From a condition to find the theoretical value of co-ordinate of a minimum of function; to compare a theoretical value to experimental, found for graphic .

Draw conclusion.

Figure 8.2

Additionally. To build theoretical and experimental graph by a computer.

For more detailed research of a minimum of function (8.4) do the additional measurings of period of oscillations in an interval with a less step (for example - ). Expect the theoretical values of period at those values. Compare a theory to the experiment, building graphic arts. Draw conclusion, in relation to justice of formulas (8.1) – (8.4).

Control questions

1. What harmonic oscillations? Write down differential equalization of harmonic oscillations and his decision.

2. What is physical pendulum? Write down the formula of the period of oscillation of the physical pendulum.

3. Formulate the theorem of Steiner.

4. Draw the graph of the dependence of period of oscillations of peg from distance between the axis of rotation and pegycenter.

Literature

1. Сивухин Д. В. Общий курс физики. – т. 1. – М.: Наука, 1980.

2. Савельев И. В. Курс общей физики.– т. 1. – М.: Наука, 1982.

Authors: M.I. Pravda, the reader, candidate of physical and mathematical sciences.

Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.

Approved by the chair of physics. Protocol № 6 from 30.03.2009 .

Date: 2015-12-24; view: 1027