
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
From (2.5) and (2.6) get the period of oscillation of the spring pendulum
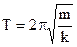 . (2.10)
. (2.10)
When load hangs on a spring, which does not carry out oscillations, it deforms a spring on the size of õî. By Hook`s law of F = mg = kxo, it is possible to find rigidity of spring
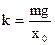 . (2.11)
. (2.11)
Then a formula (2.8) for the period of oscillations assumes an air
 (2.12), or
(2.12), or  . (2.13)
. (2.13)
Thus, experimentally measuring the period of oscillations of T and lengthening of spring of õî, from its undeformed state to position of equilibrium at the different loadings, it is possible on the angle of slope of graph of T2 = f(xo) (see a formula 2.11) to find the acceleration of the free falling. The first task is so executed.
The second task of work is executed on the basis of formula (2.8), that the linearness of dependence is checked up 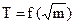 .
.
Order of execution
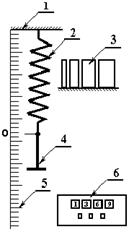
Figure 2.1
1. Varying the weights on the spring measure time of 50 oscillations by the stop-watch (once for each weight). Then calculate a period of oscillations for each measurement.
2. Represent graphically the dependence of period 
 on
on  .
.
3. Using the graph determine a rigidity of the spring.
To take off from a spring fastening of loads and to mark position of end of spring on a line (points of hang up of fastening).
1. To hang up fastening and, combining the set of loads, to change general mass of m of a spring pendulum from the least (one fastening to most, all loads is suspended). Mass of fastening is 11 g, the masses of loads see on them.
2. With the chosen mass of m to measure deformation of õî spring to position of equilibrium, and then, giving small amplitude (2 ÷ 3 sm), to measure a stop-watch time 20 oscillations. To add the results of measurings to the table 2.1. An amount of combinations of the masses must be not less 9 ÷ 10.
Table 2.1
| n | m, kg | xo, sm | t, s | T, s | T2, s2 | 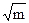 ,
kg0.5 ,
kg0.5
| 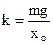
| ka |
| - | ||||||||
| - |
On results of every experience to expect rigidity of spring k on formula (2.9) and to find it mean value.
3. To build graphics: 1) Ò2 = f(xo); 2) 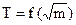
4. On lineal parts of graph (2.3) to choose for two points 1 ÷ 2 and 3 ÷ 4, to define their coordinates for to the axes, but not from a table, and after formulas (2.12) and (2.13) to expect g and k.
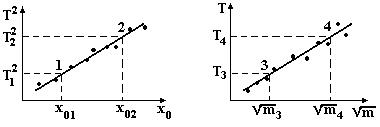
Figure 2.2
 (2.14)
(2.14) 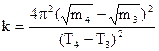 (2.15)
(2.15)
5. To draw conclusion, comparing the value of g to tabular, and k, got after a formula (2.3), with a mean value, found after a formula (2.9). In a conclusion also to mark or are line’s graphic got in experiments and if so, then what does it testify to?
Questions
1. What kind of oscillations is called harmonic? Write the dependence of deviation upon time for harmonic oscillations.
2. Give definitions for period, amplitude, frequency, cyclic frequency and phase.
3. Write the differential equation of harmonic oscillations.
4. Write the formula for period of a spring pendulum. What is a rigidity of a spring?
Authors: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol ¹ 6 from 30.03.2009 .
Date: 2015-12-24; view: 1508
| <== previous page | | | next page ==> |
| TREASURES OF CATHERINE THE GREAT | | | Laboratory work ¹ 42 |