LONGITUDINAL STABILITY

In conventional longitudinal aircraft dynamics, for instance, these are the short-period pitching oscillation (SPPO) mode and the phugoid mode. The dynamic behaviour of all systems can be considered as a collection of first-order and second-order modes. Each mode is composed of two elements. The first is one that describes the transient (time-decay and frequency) behaviour of the mode. In classical control engineering, this is the pole of the mode; in eigenstructural terms, this is the eigenvalue of the mode. The second component of each mode is a magnitude which it has at any time step; this is the residue of the mode.

The dynamic stability of perturbed longitudinal motion is mostly effectively established from knowledge of the eigenvalues of the coefficient matrix A. They can be found by solving the linear equation:

,

where I is an identity matrix of the corresponding dimension. By expanding the determinant, the longitudinal stability quartic, a fourth degree polynomial in λ, can be expressed as:

(6)

An aircraft may be said to be dynamically stable if all its eigenvalues, λ_i, being real, have negative values, or, if they be complex, have negative real parts. Zero, or positive, values of the real part of any complex eigenvalue means that the aircraft will be dynamically unstable. Eigenvalues determine the damping and natural frequencies of the linear system’s modes of motion.

It has been observed that for the majority of aircraft types, the quadratic of equation (6) invariably factorizes into two quadratic factors in the following manner:

(7)

The first factor corresponds to a mode of motion which is characterized by an oscillation of long period. The damping of this mode is usually very low, and is sometimes negative, so that the mode is unstable and the oscillation grows with time. The low frequency associated with the long period motion is defined as the natural frequency, ; the damping ratio has been denoted as . The mode is referred to as the phugoidmode.

The second factor corresponds to a rapid, relatively well-damped motion associated with the short period mode whose frequency is and damping ration is . In Fig.2 the short period pitching oscillation is shown.

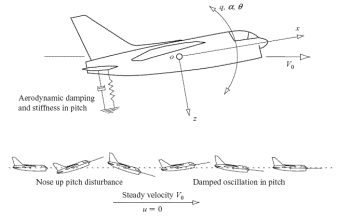
Figure 2 A stable short-period pitching oscillation

Let us consider characteristic equation of longitudinal motion of the aircraft given by equating the common denominator polynomial to zero

,

The characteristic equation is represented in form of equation (7). The first pair of complex roots is characterized by the following damping ratio and undamped natural frequency:

Undamped natural frequency: rad/s,

time constant, s

Daming ratio: .

The second pair of complex roots possesses with following damping ration and undamped natulal frequency:

Undamped natural frequency rad/s and time constant s

Daming ratio: .

Hence, it is possible to conclude that the first pair of complex root characterizes the phugoid stability mode, meanwhile the second pair of complex root characterizes the short-period pitching oscillating mode or short – period stability mode.

Theshort period mode is typically a damped oscillation in pitch about the oy axis. Whenever an aircraft is disturbed from its pitch equilibrium state the mode is excited and manifests itself as a classical second order oscillation in which the principal variables are incidence α(w), pitch rate q and pitch attitude θ. A significant feature of the mode is that the speed remains approximately constant (u=0) during a disturbance. As the period of the mode is short, inertia and momentum effects ensure that speed response in the time scale of the mode is negligible.

The phugoid mode is most commonly a lightly damped low frequency oscillation in speed u which couples into pitch attitude θ and height h. A significant feature of this mode is that the incidence α(w) remains substantially constant during a disturbance. In Fig.3 the phugoid aircraft mode is shown. However, it is clear that the phugoid appears, to a greater or lesser extent, in all of the longitudinal motion variables but the relative magnitudes of the phugoid components in incidence α(w) and in pitch rate q are very small. Typically, the undamped natural frequency of the phugoid is in the range 0.1 rad/s to 1 rad/s and the damping ratio is very low. However, the apparent damping characteristics of the mode may be substantially influenced by power effects in some aeroplanes.

Consider the development of classical phugoid motion following a small disturbance in speed as shown in Fig.3 (for more see M.V. Cook Flight Dynamics. Principles). It could be seen that the phugoid motion is classical damped harmonic motion resulting in the aircraft flying a gentle sinusoidal flight path about the nominal trimmed height datum.

Figure 3 Stable phugoid mode

Thus, summing up above given information it is possible to conclude that longitudinal characteristic modes compose the short – period and phugoid modes, respectively.

The short – period mode inherent characteristics are:

- Quick, high frequency (“short - period”);

- Well damped (few overshoots);

- Pitch and α vary.

It is necessary to point out, that responses clearly show both dynamic stability modes, the short period pitching oscillation and phugoid. However, the magnitude of each mode differs in each response variable. For example, the short period pitching oscillation is most visible as the initial transient in variables w, q and α whereas the phugoid mode is visible in all variables although the relative magnitudes vary considerably. The mode content in each of the motion variables is given most precisely by the eigenvectors.

For example, for the A-7A aircraft with state space matrix A, given below

the eigenvector matrix Vis determined as follows:

To facilitate interpretation of the eigenvector matrix, the magnitude of each component eigenvectors is calculated as follows:

Clearly, the phugoid mode is dominant in u since 0.979>>0.213, the short period mode is dominant in w since 0.977>>0.204, the short period mode is dominant in q since 0.0049>>0.0006 and the short period mode and phugoid modes content in θ are of similar order.

In Fig. 4 the short period and phugoid modes are demonstrated on the example of pitch attitude response of the Aircraft F-104 to a 1⁰ degree step of elevator

Figure 4 Pitch attitude response of the Aircraft F-104to a 1⁰ degree step of elevator

Date: 2015-12-24; view: 4327