AIRCRAFT RESPONSE TRANSFER FUNCTIONS

LABORATORY WORK № 5

AIRCRAFT RESPONSE TRANSFER FUNCTIONS

AIRCRAFT STABILITY AND DYNAMICS

BRIEF THEORETICAL REVIEW

Dynamic stability is a very important field for the understanding of aircraft flying and handling qualities.

While static stability determines the steady state, or trim, of an aircraft, the dynamic stability is related to the dynamic, or transient, part of the aircraft response to pilot or disturbance inputs. Therefore, although the steady state is the ultimate objective of a pilot, the way an aircraft behaves to reach that end, i.e. the transient response, may be more determinative for pilots when assessing a certain configuration for accomplishing a specified task. Since dynamic stability defines the transient response of a system its characteristics are not dependent on just a few basic aerodynamic parameters, but on the more complex relationships and interaction of all characteristics. The equations of motion represent the complete analytical source of an aircraft response, both transient and steady state, to pilot inputs. However, the analysis of the complete non-linear equations of motion is very complex. Thus, the usual approach is to assume small perturbations and to linearize the equations of motion around a flight condition, to obtain the well-known state space model. A further simplification is to separate the longitudinal motion from the lateral – directional motion due to the symmetry of the airplane.

The possibility of separating the longitudinal and lateral- directional stability aircraft motion makes it easier to analyze and understand the aircraft behaviour.

AIRCRAFT RESPONSE TRANSFER FUNCTIONS

Aircraft response transfer functions describe the dynamic relationships between the input and output variables. The relationships are indicated diagrammatically in Fig.1 and clearly, a number of possible input–output relationships exist. When the mathematical model of the aircraft comprises the decoupled small perturbation equations of motion, transfer functions relating longitudinal input variables to lateral output variables do not exist and vice versa. This may not necessarily be the case when the aircraft is described by a fully coupled set of small perturbation equations of motion. For example, such a description is quite usual when modelling the helicopter. All transfer functions are written as a ratio of two polynomials in the Laplace operator s. All proper transfer functions have a numerator polynomial which is at least one order less than the denominator polynomial although, occasionally, improper transfer functions crop up in aircraft applications. For example, the transfer function describing acceleration response to an input variable is improper, the numerator and denominator polynomials are of the same order. Care is needed when working with improper transfer functions as sometimes the computational tools are unable to deal with them correctly. Clearly, this is a situation where some understanding of the physical meaning of the transfer function can be of considerable advantage.

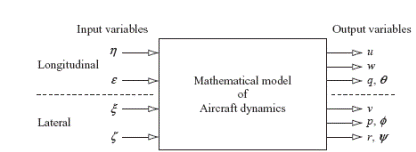
Figure 1 Aircraft input – output relationships

A shorthand notation is used to represent aircraft response transfer functions. For example, pitch attitude θ(s) response to elevator η(s) is denoted:

,

where is the unique numerator polynomial in s relating pitch attitude response to elevator input and is the denominator polynomial in s which is common to all of the longitudinal response transfer functions.

The denominator polynomial Δ(s) is called the characteristic polynomial and when equated to zero defines the characteristic equation. Thus, Δ(s) completely describes the longitudinal or lateral stability characteristics of the aeroplane as appropriate and the roots, or poles, of Δ(s) describe the stability modes of the aeroplane. Thus, the stability characteristics of an aeroplane can be determined simply on inspection of the response transfer functions.

Date: 2015-12-24; view: 1359