
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
STANDARD TASK FOR LABORATORY WORK 5
The equation of motion referred to body axis system, arranged in state space form is given with quadruple of matrices A, B, C, D. It is necessary:
- obtain the reduced order model for short period and phugoid modes;
- evaluate by hand the transfer function describing pitch attitude response to elevator deflection for short period mode;
- find the longitudinal eigenvalues and eigenvectors and compare with the results obtained by using short period and phugoid modes, respectively;
- determine the period of the short period and phugoid modes;
- write down the longitudinal characteristic equation and state whether the airplane is stable or not.
INDIVIDUAL VARIANTS
Variant 1
The equation of motions for the Ling-Temco-Vought A-7A Corsair II aircraft is given in state space form. The state space vector composes the following variables:
x=[u w q θ]T
 ;
; 
Variant 2
The equation of motions for the Corsair II aircraft is given in state space form. The state space vector composes the following variables:
x=[u w q θ]T
 ;
; 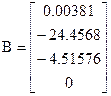
Variant 3
The longitudinal data for the Douglas A-4D Skyhawk flying at Mach 1.0 at 15,000 ft are given as follows:
Speed of sound at 15,000 ft 1058 ft/s.
Xw=-0.0251 1/s; 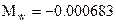 1/ft;
1/ft;
Xu=-0.1343 1/s; Mw=-0.1072;
Zw=-1.892 1/s; Mu=0.00263 1/fts;
Zu=-0.0487 1/s; Mq=-2.455 1/s;
 ft/rad/s2;
ft/rad/s2;  ft/rad/s2;
ft/rad/s2;  1/s2;
1/s2;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value.
The state space vector composes the following variables: x=[u w q θ]T Using state space approach it is necessary to obtain the state space matrices for the Skyhawk and perform the above given task;
Variant 4
The equation of motions for the Lockheed F-104 Straightfighter aircraft is given in state space form. The state space vector composes the following variables:
x=[u w q θ]T
 ;
; 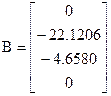
Variant 5
The equation of motions for the McDonnell F-4C Phantom aircraft is given in state space form. The state space vector composes the following variables: x=[u w q θ]T
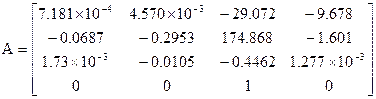 ;
; 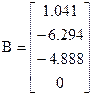
Variant 6
The equation of motions for the X-15 aircraft is given in state space form. The flight condition assumed corresponds with Mach 2.0 at an altitude of 60,000 ft. The state space vector composes the following variables:
x=[u w q θ]T
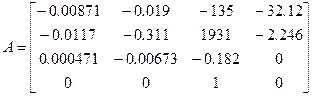 ;
; 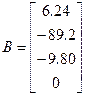
Variant 7
The longitudinal data for the Republic F- 105 Thunderchief flying at 35,000 ft are given as follows:
Xw=0.0714; Xu=-0.0599; Xq=0; Zq=0;
Zw=-4.1188; Zu=-0.1427; Mw=-0.8021; Mu=0;
 ; Mq=-4.1303;
; Mq=-4.1303;  ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value.
The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Republic F- 105 Thunderchief and perform the above given task;
Variant 8
The longitudinal data for the canard configured FBW combat aircraft flying at sea level altitude are given as follows:
Xw=0.260; Xu=0.050; Xq=0; Zq=-1.200;
Zw=-2.800;  ; Zu=-1.200; Mw=0.282;
; Zu=-1.200; Mw=0.282;
Mu=0.003;  ; Mq=-0.500;
; Mq=-0.500;  ;
;
 ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the canard configured FBW combat aircraft and perform the above given task;
Variant 9
The equation of motions for the McDonnell Douglas F-4C Phantom aircraft is given in state space form. The flight condition assumed corresponds with Mach 1.0 at a sea level altitude. The state space vector composes the following variables:
x=[u w q θ]T
 ;
; 
Variant 10
The longitudinal data for the Foxtrot - a twin – engined, jet fighter / bomber aircraft flying at Mach 0.206 at sea level altitude are given as follows:
Uo=70 m/s;
Xw=0.14; Xu=-0.042; Xq=0; Zq=-0.76;
Zw=-0.452; Zu=-0.177; Mw=-0.006; Mu=-0.0024;
 ; Mq=-0.317;
; Mq=-0.317;  ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the bomber aircraft and perform the above given task.
Variant 11
The longitudinal data for the Foxtrot - a twin – engined, jet fighter / bomber aircraft flying at Mach 0.9 at 10650 m altitude are given as follows:
Uo=265 m/s;
Xu=-0.009; Xw=0.016; Xq=0; Zq=-0.88;
Zw=-0.547; Zu=-0.088; Mw=-0.03; Mu=-0.008;
 ; Mq=-0.487;
; Mq=-0.487;  ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the bomber aircraft and perform the above given task.
Variant 12
The longitudinal data for the Foxtrot - a twin – engined, jet fighter / bomber aircraft flying at Mach 1.2 at 10650 m altitude are given as follows:
Uo=350 m/s;
Xu=-0.0135; Xw=0.006; Xq=0; Zq=-1.25;
Zw=-0.727; Zu=0.0125; Mw=-0.08; Mu=0.009;
 ; Mq=-0.745;
; Mq=-0.745;  ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the bomber aircraft and perform the above given task.
Variant 13
The longitudinal data for the Foxtrot - a twin – engined, jet fighter / bomber aircraft flying at Mach 2.15 at 13700 m altitude are given as follows:
Uo=650 m/s;
Xu=0.016; Xw=0.004; Xq=0; Zq=-0.39;
Zw=-0.494; Zu=-0.001; Mw=-0.07; Mu=0.07;
 ; Mq=-0.41;
; Mq=-0.41;  ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the bomber aircraft and perform the above given task.
Variant 14
The longitudinal data for the Charlie a very large, four –engined, passenger jet aircraft flying at Mach 0.198 at sea level are given as follows:
Uo=65 m/s;
Xu=-0.021; Xw=0.122; Zq=-1.9; Zw=-0.512;
Zu=-0.2; Mw=-0.006; Mu=0.000036; Mq=-0.357;

 ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Charlie aircraft and perform the above given task.
Variant 15
The longitudinal data for the Charlie a very large, four –engined, passenger jet aircraft flying at Mach 0.5 at 6100 m altitude are given as follows:
Uo=158 m/s;
Xu=0.003; Xw=0.078; Zq=-1.95; Zw=-0.433;
Zu=-0.07; Mw=-0.006; Mu=0.00008; Mq=-0.421;

 ;
; 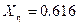 ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Charlie aircraft and perform the above given task.
Variant 16
The longitudinal data for the Charlie a very large, four –engined, passenger jet aircraft flying at Mach 0.8 at 6100 m altitude are given as follows:
Uo=250 m/s;
Xu=-0.0002; Xw=0.026; Zq=-3.04; Zw=-0.624;
Zu=-0.09; Mw=-0.005; Mu=-0.00007; Mq=-0.668;
 ;
;  ;
;  ;
; 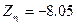 ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Charlie aircraft and perform the above given task.
Variant 17
The longitudinal data for the Charlie a very large, four –engined, passenger jet aircraft flying at Mach 0.8 at 12200 m altitude are given as follows:
Uo=250 m/s;
Xu=0.0002; Xw=0.039; Zq=-1.57; Zw=-0.317;
Zu=-0.07; Mw=-0.003; Mu=-0.00006; Mq=-0.339;
 ;
;  ;
; 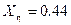 ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Charlie aircraft and perform the above given task.
Variant 18
The longitudinal data for the Delta a very large, four –engined, cargo jet aircraft flying at Mach 0.22 at sea level altitude are given as follows:
Uo=75 m/s;
Xu=-0.02; Xw=0.1; Zw=-0.634; Zu=-0.23;
Mw=-0.005; Mu=-2.55x10-5; Mq=-0.61;  ;
;
 ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Delta aircraft and perform the above given task.
Variant 19
The longitudinal data for the Delta a very large, four – engined, cargo jet aircraft flying at Mach 0.6 at 6100m altitude are given as follows:
Uo=190 m/s;
Xu=-0.003; Xw=0.04; Zw=-0.618; Zu=-0.08;
Mw=-0.007; Mu=3.28x10-4; Mq=-0.77;  ;
;
 ;
;  ;
;  ;
;
The derivatives are not quoted are assumed to be insignificant and are given a zeros value. The state space vector composes the following variables: x=[u w q θ]T
Using state space approach it is necessary to obtain the state space matrices for the Delta aircraft and perform the above given task.
Date: 2015-12-24; view: 1563
| <== previous page | | | next page ==> |
| LONGITUDINAL STABILITY | | | Entrepreneur and your qualities |