
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
CUADRO COMPARATIVO ENTRE EL TRANSFORMADOR Y EL MOTOR DE INDUCCION
| TRANSFORMADOR | MOTOR DE INDUCCION |
| § Flujo principal que enlaza los dos devanados (primario y secundario). | Flujo principal (giratorio) que enlaza los dos devanados (Estator y Rotor) |
| § Trayectoria magnética: · núcleo magnético. | § Trayectoria magnética: · núcleo magnético del estator (1) · dientes del estator (2) · entrehierro (2) · dientes del rotor (2) · núcleo magnético del rotor (1) |
| § El flujo de dispersión estaba presente en el devanado primario. | § Flujos de dispersión: · Flujo de dispersión de la ranura. · Flujo de dispersión en la parte superior de los dientes del estator. · Flujo de dispersión en los cabezales de la bobina · Flujo de dispersión diferencial (armónico) |
ANALISIS DEL COMPORTAMIENTO DE LA MAQUINA DE INDUCCION
Un arrollamiento de ca produce una onda de FMM fundamental, la longitud de la cual es dos veces el paso polar de la máquina, y ondas FMM armónicas. Unicamente el flujo producido por la onda de la FMM fundamental produce el par motor útil de la máquina. Los flujos armónicos son flujos parásitos y se consideran como un flujo de dispersión. Este flujo de dispersión es conocido como el flujo de dispersión diferencial o armónico.

 Kd1 = (Senqa/2)/(qSena/2) Fundamental Trabajo Util
Kd1 = (Senqa/2)/(qSena/2) Fundamental Trabajo Util

 Kdn = (Sennqa/2)/(qSenan/2) Armónicas Pérdidas
Kdn = (Sennqa/2)/(qSenan/2) Armónicas Pérdidas
Kp1 = Senp/2w/2
Kpn = Sennp/2w/2
El flujo principal induce una tensión no únicamente en el arrollamiento del estator sino también en el arrollamiento del rotor. La velocidad del flujo giratorio producido por las corrientes del estator es, con respecto al estator:

ns = 120f1/p
Esta velocidad es conocida como velocidad síncrona. Generalmente, cuando el rotor gira con una velocidad n en la dirección del flujo giratorio, la velocidad relativa entre el flujo giratorio y el arrollamiento del rotor es ns - n. Ya que el rotor se considera aquí en reposo n = 0, la velocidad relativa entre el flujo giratorio y el rotor es igual a ns, esto es, la frecuencia de la fem inducida en el arrollamiento del rotor es:

f2 = nsp/120 = f1
Entonces, la fem inducida en el arrollamiento del rotor en reposo es:

E2 = 4.44N2f1fKdp210-8
La relación de las fems inducidas en ambos arrollamientos por el flujo principal es igual a la relación de sus espiras efectivas.

E2/E1 = N2Kdp2/N1Kdp1
b) El motor de inducción con los anillos cerrados pero su rotor bloqueado mecánicamente.-
c)
Im = If + Ih+e
 0
0
V1 = -E1 + I1r1 + jI1x1 E2 = V2 + I2’r2 + jI2’x2
FMM1 = 0.9m1(N1/p)Kdp1I1
FMM2 = 0.9m2(N2/p)Kdp2I2
Al cerrar los anillos circula una corriente I2, y en el rotor existirán flujos de dispersión en:
- Ranuras,
- Aberturas
- Cabezales
- Flujo de dispersión diferencial
Ambas FMM están estacionarias y esta condición es necesaria para producir un torque uniforme.
CANTIDADES DEL ROTOR REFERIDAS AL ESTATOR:
En el rotor existe un devanado ficticio:
N1
I2’
E2’
r2’
X2’
Condiciones:
Se deben mantener:
1) FMM2 (Fuerza Magnetomotiva):
0.9m2(N2/p)Kdp2I2 = 0.9m1(N1/p)Kdp1I2’
m2Kdp2N2 / m1Kdp1N1 = I2’/I2

I2’ = (m2Kdp2N2 / m1Kdp1N1)I2
2) KVA2 (Potencia Aparente):
m2E2I2 = m1I2’E2’ = m1E2’(m2Kdp2N2 / m1Kdp1N1)I2

E2’ = (N1Kdp1 / N2Kdp2)E2 = E1
Con anillos abiertos:
E1/E2 = N1Kdp1/N2Kdp2

E1 = (N1Kdp1/N2Kdp2)E2
3) I22r2 (Pérdidas de Joule):
m2I22r2 = m1I2’2r2’
m2I22r2 = m1(m2Kdp2N2 I2 / m1Kdp1N1)2 r2’

r2’ = (m1/m2)( N1Kdp1/N2Kdp2)2r2
4) ½ L2 (Energía):
m2(1/2 L2I22) = m1 (1/2 L2’I2’2)
Si se multiplica por 2pf = w
m2x2I22 = m1x2’I2’2
d) Motor de Inducción cuando gira.-
 Cuando el rotor gira: n < ns diferencia entre el rotor y el flujo para la producción de f.e.m. en el rotor.
Cuando el rotor gira: n < ns diferencia entre el rotor y el flujo para la producción de f.e.m. en el rotor.
Donde n: Velocidad del rotor, y es en el mismo sentido que la del campo giratorio.


 E2 ns f1 E2s = (ns – n)/ ns E2
E2 ns f1 E2s = (ns – n)/ ns E2


 E2s ns-n f2
E2s ns-n f2
Con cantidades referidas:

E2s’ = E2’(ns – n)/ns
Calculo el valor de f2 con la fórmula anterior:

f2 = f1 (ns – n)/ns
Donde el deslizamiento S (variable) es:

S = (ns – n) /ns
 |
La corriente I1 establece una FMM1.
Se concluye que las FMM del estator y del rotor en funcionamiento se mantienen estacionarias produciéndose un torque uniforme.
ROTOR JAULA DE ARDILLA SU NUMERO DE POLOS Y FASES
Considerando el rotor, se debe tener que el número de polos del rotor es el mismo que los del estator. Estator y rotor deben tener el mismo número de polos en todas las máquinas eléctricas (p1 = p2). En el rotor de fase devanada la igualdad del número de polos se lleva a cabo devanando simplemente el rotor para el mismo número de polos que el estator. El rotor jaula de ardilla produce automáticamente el mismo número de polos que el estator.
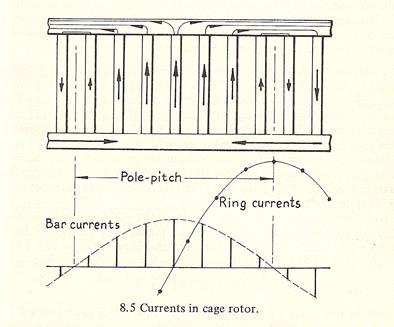
En la figura, el flujo giratorio está distribuido senoidalmente. Este flujo se mueve con la velocidad ns mientras que el rotor gira a la velocidad n. Con respecto al rotor, el flujo giratorio se mueve a una velocidad relativa ns-n.
 |
e
 |
B se mueve en el entrehierro
 i
i
 |  | ||||||||||
 |  |  |  | ||||||||

Para demostrar que p1 = p2 se aplica la Ley de Faraday:

e = Blv.10-8
Donde: B = f/A [Gauss]
l = longitud [centímetros]
v = velocidad [centímetros/segundos]
Entonces, las f.e.m.s inducidas en las barras individuales de la jaula de ardilla también están distribuidas senoidalmente. Se supone que la velocidad del rotor n es muy cercana a la velocidad síncrona ns, como es generalmente el caso para funcionamiento a la salida nominal. La reactancia de dispersión del rotor sx2’ viene a ser entonces muy pequeña, y puede suponerse entonces, que la corriente y la f.e.m. de las barras individuales del rotor están en fase. Por lo tanto, las f.e.m.s de las barras individuales de la figura representan, a otra escala, las corrientes en las barras individuales, y si se indican las corrientes por cruces bajo la media onda positiva de la curva B, deben indicarse por puntos bajo la media onda negativa de la curva B. Se ve que la onda de flujo produce una distribución de corriente de dos polos y también aquí una distribución de f.e.m.s de dos polos en el rotor jaula de ardilla. Ya que el número de polos de la onda del flujo es el mismo que para el arrollamiento del estator, el rotor jaula de ardilla produce el mismo número de polos que los del estator.
 |
Las f.e.m.s de las barras individuales son funciones senoidales del tiempo, ya que B es senoidal. Como tales pueden representarse por vectores. El ángulo de tiempo entre los vectores que representan dos barras adyacentes es igual al ángulo en el espacio entre las dos barras (ángulo de ranura as). El número total de vectores es igual al número de barras (Q2). La figura muestra el diagrama vectorial de un rotor jaula de ardilla con 15 barras. Se ve que el arrollamiento jaula de ardilla es un arrollamiento polifásico con m2 = Q2 fases. El número de espiras por fase es N = ½, debido a que cada fase consiste en un conductor. Los factores de distribución y de paso son iguales a 1. De este modo, para el rotor jaula de ardilla:

m2 = Q2 ; N2 = ½ ; Kd2 = 1 ; Kp2 = 1
Las relaciones anteriores han sido deducidas en la suposición de que el estator tenía un arrollamiento de dos polos. Si el número de polos es p, entonces:

m2 = 2Q2/p ; N2 = ½ ; Kd2 = 1 ;Kp2 = 1
Introducimos estos valores en las fórmulas deducidas para las máquinas con rotor devanado:
E2 = 4.44N2f1fKdp210-8
E2/E1 = N2Kdp2/N1Kdp1
FMM2 = 0.9m2(N2/p)Kdp2I2
Date: 2015-12-24; view: 995
| <== previous page | | | next page ==> |
| FUERZA MAGNETOMOTIVA (FMM) EN LOS DEVANADOS DE CORRIENTE ALTERNA | | | DIAGRAMA FASORIAL Y CIRCUITO EQUIVALENTE DEL MOTOR POLIFASICO DE INDUCCION |