MAIN Properties of Definite Integrals

Properties of Definite Integrals

P1. The value of the definite integral of a given function is a real number, depending on its lower and upper limits only, and is independent of the choice of the variable of integration, i.e.

.

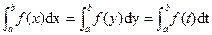P2.

P3.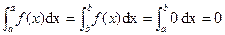

P4. Let , then .

P5. Comparison of two integrals

If 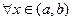, then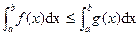

P6. Rules of Integration

If are continuous function o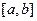n then

(a) for some constant k.

(b) .

Newton – Leibniz formula

Comparing the two formulas of the curvilinear trapezoid area, we make the conclusion: if F ( x ) is primitive for the function f ( x ) on a segment [ a, b ] , then

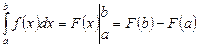
This is the famous Newton – Leibniz formula. It is valid for any function f ( x ), which is continuous on a segment [ a , b ] .

(i) If 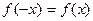(Even Function)

then .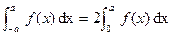

(ii) If 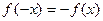(Odd Function)

Then .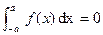

Integration by substitution

If the function u = g(x) has a continuous derivative on [a, b] and f is continuous on the range of g, then

Steps for Integrating by Substitution—Definite Integrals

1. Choose a substitution u = g(x), such as the inner part of a composite function.

2. Compute 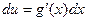. Compute new u-limits of integration g(a) and g(b).

3. Re-write the integral in terms of u and du, with the u-limits of integration.

4. Find the resulting integral in terms of u.

5. Evaluate using the u-limits. No need to switch back to x’s!

Date: 2015-01-02; view: 1268