
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Type 5.
Other rational expressions with the irrational function 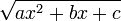
1. If 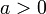 , we can use
, we can use 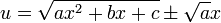 .
.
2. If  , we can use
, we can use  .
.
3. If 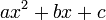 can be factored as
can be factored as 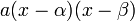 , we can use
, we can use 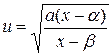 .
.
4. If 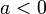 and
and 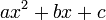 can be factored as
can be factored as 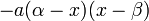 , we can use
, we can use 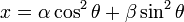
Frequently occuring integrals of irrational functions are: 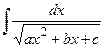 , where
, where 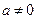 and
and 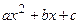 is possitive on an interval. We can exclude the case, that the polynomial
is possitive on an interval. We can exclude the case, that the polynomial 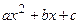 has a double root.
has a double root.
Taking the factor 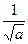 (if
(if 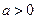 ) or
) or 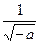 (if
(if 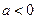 ) we reduce the integral to the form
) we reduce the integral to the form 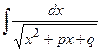 or
or 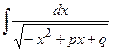 , leading (by means of substitution) to the integrals:
, leading (by means of substitution) to the integrals:
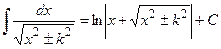 or
or 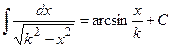 , respectively.
, respectively.
3. Integration of TRIGONOMETRIC functions
1. Given an integral 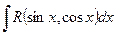 , i.e. the integrand is a rational function in terms of
, i.e. the integrand is a rational function in terms of 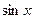 and
and 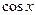 . By the substitution
. By the substitution 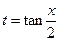 the integral is reduced to an integral of a rational function. If
the integral is reduced to an integral of a rational function. If 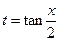 , then
, then 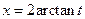 ,
, 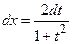 ,
,  and
and 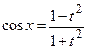 .
.
2. If 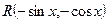 =
= 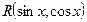 , then
, then 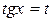 .
.
3. If  = -
= - 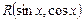 , then
, then 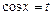 .
.
If 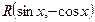 =-
=- 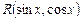 , then
, then 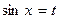 .
.
4. 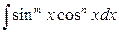 , ò and ï – even non-negative integers, then
, ò and ï – even non-negative integers, then  ,
, 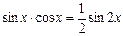 .
.
5. For integrals 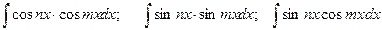 we use following formulas:
we use following formulas:
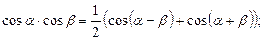
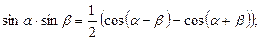
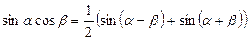
6.  , then
, then  and
and 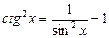 .
.
Date: 2015-01-02; view: 1503
| <== previous page | | | next page ==> |
| Integration of simple rational fractions. Integration of rational fractions | | | MAIN Properties of Definite Integrals |