Function. function limit. Fundamental theorems on limits. Infinitely small and infinitely large quantities. The ends

LECTURE PLAN:

1. Function limit

2. Infinitely small and infinitely large quantities

3. Main theorems about limits and their applications

4. Continuity of function

The limit of a sequence.

Definition. A sequence is an infinite set of terms, each of which is assigned a number. The terms of a sequence must obey a certain law.

х₁,х₂,х₃,х₄,…,х_n,….

Example.

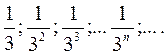
Definition. A number а is called the limit of a sequence if, for any >0, there exists a number N() depending on  , such

for n>N,

Notation:

.

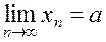Example.

.

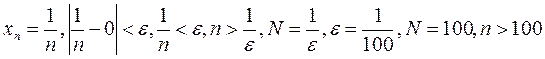Definition. The limit of a variable х is a number а such that for any >0, there exists an х starting with which all х satisfy the inequalities

.

Notation:

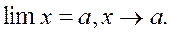
2

а– а а+

х(а–;а+)

Properties:

1. The limit of a constant number equals this number.

2. A variable can not have two different limits.

3. Some variables have no limit.

Example. 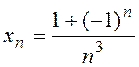. Assigning integer values to n, we obtain: 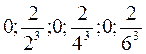etc.; i.e. this variable has no limit.

Definition. We say that х tends to infinity if, for any number М, there exists an х such that, starting it,

.

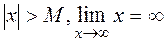(a) M>0, x>M, x;

(b) M<0, x<–M, x –.

Example. x_n=n²+1 ; as n, х_n tends to infinity.

The limit of a function. Suppose that y=f(x) is a function defined on a domain D containing a point а: аD.

Definition. A number b is called the limit of the function f(x) as х а if, for any given >0, there exists a small positive  depending on  (()>0) such that, for any х satisfying the inequality , 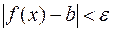. Notation:

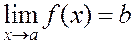. (1)

Example. Find the limit of f(x)=5x–1 as x2, and determine .

,

,

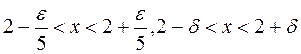i.e., .

To find , we must find x from the inequality for the function and substitute it in the inequality for the variable.

Definition. The left limit of a function f(x) as x a is the limit of f(x) as x a, and х<а. Notation:

.

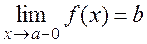Definition. The right limit of a function f(x) as x a, is the limit of f(x) as x a, and х>а. Notation:

.

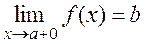If the left limit equals the right limit and some number b, then b is the limit of the function as x a.

Example.

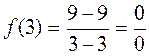; an indeterminacy, although the limit exists:

.

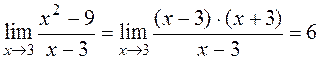Definition. A number b is called the limit of f(x) as х if, for any >0, there exists a (large) number N depending on  such that 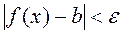for any .

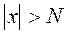Notation:

.

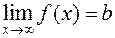Infinitesimals and bounded functions.

Definition. A function f(x) is said to be infinitesimals as х а if, for any М, there exists a  such that whenever .

Notation:

.

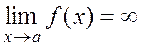Definitions. 1. A function f(x) is said to be bounded on a domain D if, for any х from D,

|f(x)|M.

For example, f(x)=cosx , |cosx|1, M=1,

.

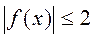If this condition is not satisfied, then the function is said to be unbounded, i.e., this function is an infinite quantity.

2. A function f(x) is said to be bounded as х а if, for any х from a neighborhood of а, |f(x)|M.

3. A function f(x) is said to be bounded as х  if, for any х>N, |f(x)|M.

Theorem I. If a function f(x) has a finite limit as xa then f(x) is bounded as x a.

Theorem II. If a function has a limit as х а and this limit is not equal to zero, then 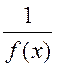is bounded as х а.

The infinitesimals and their properties.

Definition 1. A function (х) is called an infinitesimal as х а if

.

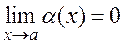Definition 2. A function (х) is called an infinitesimal as х а if, for all х( а-; а+),

.

These two definitions are equivalent, i.e., we can obtain the second definition from the first and vice versa. (Prove this).

Theorem I. If a function f(x) is represented as the sum of a constant number and an infinitesimal, i.e.,

f(x)=b+(x), (2)

then it has a limit:

.

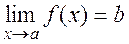Conversely, if a function f(x) has limit b, then the function can be represented in the form (2).

Theorem II. If (х) is an infinitesimal as х а, then 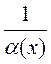is an infinite quantity.

Theorem III. The sum of finitely many infinitesimals is an infinitesimal:

₁(х) + ₂(х) + ₃(х) + … + _к(х)= (х).

Theorem IV. The product (x)^.z(x) of an infinitesimal (х) by a bounded function z(x) as x a is an infinitesimal.

Corollary. The product of infinitesimals is an even smaller quantity.

Theorem V. An infinitesimal divided by a function having nonzero limit as х а is infinitesimal, i.e., if

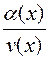, then is an infinitesimal.

Date: 2015-01-02; view: 2195