Tangent lines to a parabola. Given a point М0(х0,у0) on a parabola, it is required to write the equation of a tangent to the parabola at this point.

Let us find the slope of the tangent:

,

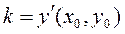To this end, we differentiate equation (20) as an implicit function:

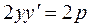, whence 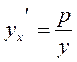, or .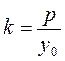

Substituting this into the equation of a straight line with given slope, we obtain

; .

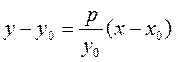Since the point М₀ (х_0;у₀) belongs to the parabola, its coordinates satisfy the equation of the parabola:

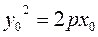; or .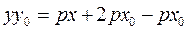

Thus, we obtain the equation of a tangent to the parabola

.

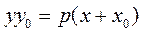Example. Write the classical equation of the parabola with directrix х=–5 . The parabola is given by the equation 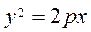, and the directrix by the equation 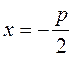, which means that and р=10.

Then, the required equation of a parabola is .

Definition. The locus of points for which the ratio of the distances to focal radii to the distances to the corresponding directrices is constant and equal to the eccentricity

, which is

(1) less than 1, then it is called an ellipse;

(2) larger than 1, is called a hyperbola;

(3) equal to 1, is called a parabola.

A General Equation of a Second-Order Curve and Its Classical Form

Definition. An equation of the form

(21)

is called a general equation of a second-order curve.

Assigning particular values to the coefficients, we obtain the above equations of a hyperbola, an ellipse, and a parabola.

Date: 2015-01-02; view: 1749