
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Parabola
Definition. The locus of points for which the distance to a fixed point equals the distance to a given straight line (a directrix) is called a parabola.
 Let us draw the perpendicular through a fixed point to the given straight line and take it for the x-axis. From the middle point of the segment joining the focus to the given straight line we draw a perpendicular and take it for the y-axis.
Let us draw the perpendicular through a fixed point to the given straight line and take it for the x-axis. From the middle point of the segment joining the focus to the given straight line we draw a perpendicular and take it for the y-axis.


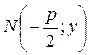 p Ì(õ;ó)
p Ì(õ;ó)
r
 |
0 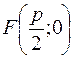 x
x
To derive the equation of the parabola, we take an arbitrary point Ì(õ;ó) on it and write down the characteristic feature of a parabola as a mathematical formula.
The distance from the focus to the directrex is called the parameter of the parabola and denoted by p. Let us find the distance from the point Ì(õ;ó) to the focus:
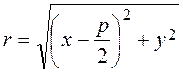 ,
,
and 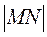 =
= 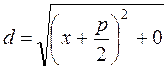 .
.
By definition, these distances are equal:
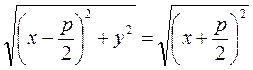 .
.
Let us transform this, relation by squaring both sides:
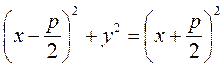 ;
;  .
.
We obtain
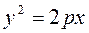 . (20)
. (20)
This is the classical equation of a parabola.
The parabola passes through the origin (0;0), because it satisfies equation (20).
Suppose that the parameter is a positive number ð>0; then, since ó2>0, we have x>0, and the parabola is contained in the right half-plane. If p<0, then x<0, and the parabola is contained in the left half-plane

 y ó
y ó
p>0 p<0
0 x 0 õ
M0(x0,y0)
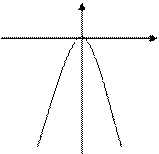
Consider the equation of a parabola in the “school” form 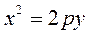 . Let us analyze this equation by analogy with (20): if p>0, then y>0, and the branches of the parabola are directed upward; if p<0, then y<0, and the branches of the parabola are directed downward.
. Let us analyze this equation by analogy with (20): if p>0, then y>0, and the branches of the parabola are directed upward; if p<0, then y<0, and the branches of the parabola are directed downward.
 p>0 y p<0 y
p>0 y p<0 y
0 x
0 x
The eccentricity of the parabola, that is, the ratio of the focal radius to the distance from a point to the directrix, equals 1, i.e.,
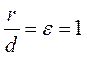 .
.
Date: 2015-01-02; view: 1402