
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
As a result, we obtain

 ;
;  .
.
By definition,  is the eccentricity of the hyperbola; we have
is the eccentricity of the hyperbola; we have 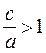 , because ñ>à.
, because ñ>à.


 By analogy with an ellipse, the directrices of a hyperbola are determined by the equations
By analogy with an ellipse, the directrices of a hyperbola are determined by the equations 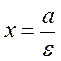 and
and  .
.
y 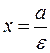

M1(–à;0) 0 M2(à;0) x
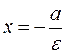
Since the eccentricity of a hyperbola is 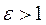 , it follows that the directrix is
, it follows that the directrix is 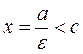 ; i.e., the directrices lie between the two vertices.
; i.e., the directrices lie between the two vertices.
The ratios of the focal radii to the corresponding distances from an arbitrary point of the hyperbola to the directrices is constant and equals the eccentricity:
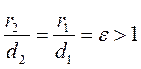 .
.
Tangent lines to a hyperbola. Suppose given, the equation of a hyperbola and a point Ì0(õ0,ó0) on it:
 .
.
As is known, the equation of a tangent to a curve is
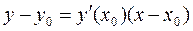 .
.
Let us differentiate the equation of a hyperbola as an implicit function:
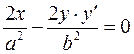 ; we obtain
; we obtain  , or
, or  .
.
Substituting, we obtain the equation of the tangent line:
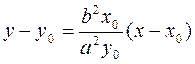 ,
,
Let us transform it:
 ;
;
 . Dividing by
. Dividing by 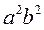 , we obtain
, we obtain
 .
.
Since the point Ì0 belongs to the hyperbola, its coordinates must satisfy the equation of the hyperbola, and, the right-hand side equals (–1) .
Thus, the equation of a tangent to a hyperbola is
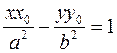 .
.
Example. Write the equation of the hyperbola with real semi axis 4 and foci at the points F1(–5;0) and F2(5;0).
Formula (19) gives
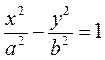
We have  and
and 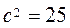 ; thus
; thus 
 –
–  =25–16=9.
=25–16=9.
The required classical equation of the hyperbola is
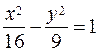 .
.
Date: 2015-01-02; view: 1261
| <== previous page | | | next page ==> |
| Asymptotes of a Hyperbola | | | Parabola |