STRAIGHT LINES IN SPACE

The Vector, Parametric, Canonical, and General Equations of a Straight Line

The position of a straight line in space is determined by a point 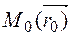on this line and a vector parallel to the line. Let us write an

equation of such a line in space.

z

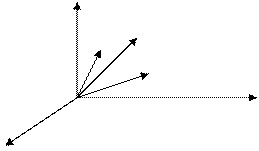
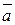
0 y

x

To this end, we take an arbitrary point 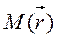on the line, join М₀ and М to the origin, and find the coordinates of the radius-vectors

,

.

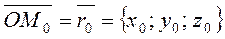It is seen from the figure, that .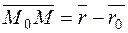

If the point М belongs to the straight line, then the vectors 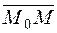and 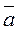are collinear.

Consequently, these vectors meet the collinearity condition

,

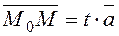where t is a parameter.

Let us write the collinearity condition in the form

; (*)

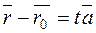equation (*) is the vector equation of the given line.

Suppose given the coordinates of the point M₀(x₀,y₀,z₀) and the direction vector 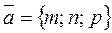. Let us write the left-hand side of equation (*) in the vector form

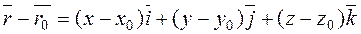
the direction vector is

.

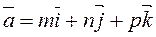Let us represent equation (*) in the form

.

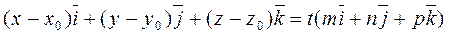Equating the respective coefficients of the unit vectors on the right- and left- sides, we obtain parametric equations of the straight line:

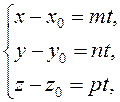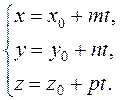or (27)

Eliminating the parameter t, we obtain the canonical equations of a straight line:

. (28)

Example. Write the canonical equations of the straight line passing through the point 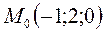parallel to the vector 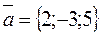. We compose the canonical equation by formula (28):

.

Equating each fraction to a parameter t, we obtain the parametric equations of the line:

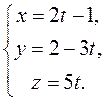
The general equation of a straight line in space. Since a straight line in space is represented as the intersection of two planes, the general equation of a straight line in space has the form of a system

where the first and the second equations are the equations of the corresponding planes.

It is always possible to transform the general equation of a straight line into a canonical equation and vice versa.

Since the direction of 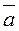is perpendicular to those of the vectors and , it follows that

,

i.e., the canonical equation is

.

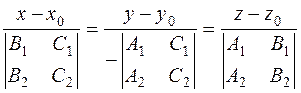The angle between straight lines in space. The parallelism and perpendicularity conditions for straight lines. Let us find the angle between intersecting right lines given by their canonical equations

; .

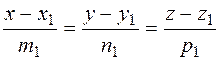The angle between these two lines is equal to the angle between their direction vectors

; ,

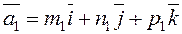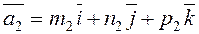i.e.,

.

The parallelism and perpendicularity conditions for right lines coincide with the collinearity and perpendicularity conditions of their direction vectors 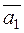and .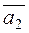

If straight lines are perpendicular, then 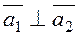, i.e., 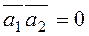, and the perpendicularity condition is

.

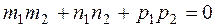If straight lines are parallel, then the vector 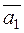is collinear to 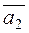, i.e., their coordinates are proportional, and the proportionality condition is

.

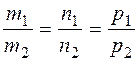Date: 2015-01-02; view: 2398