CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Since, the point belongs to the plane, its coordinates satisfy the general equation of the plane, and
z M3
M2 y
M1
õ 
.
Therefore,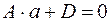 
; 
.
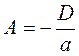By analogy, we obtain
; 
; 
,
; 
; 
.
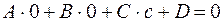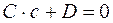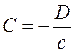Substituting the obtained values of the coefficients À,B, and C into the general equation of the plane, we obtain
,
which gives, after the reduction by D, the three-intercept equation of the plane:
.
The equation of a plane passing through three points. Suppose given, three points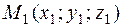 
, 
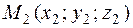, and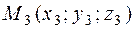 
. As is known form elementary geometry, there exists a unique plane passing through these points. It is required to write its equation.
Following the general scheme, of we take an arbitrary point M(x;y;z) in the plane.
z M2
M1 M(x;y;z)
M3
y
0
x
The characteristic feature of a plane is that if a point Ì belongs to the plane, then the three vectors
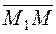={x–x1;y–y1; z–z1},
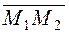= {x2–x1;y2–y1;z2–z1},
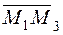={x3–x1;y3–y1;z3–z1},
are coplanar.
Therefore, the triple product of these vectors must be zero:
.
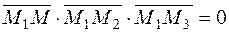Expressing the triple product in terns of coordinates, we obtain an equation of the plane, passing through the three given points:
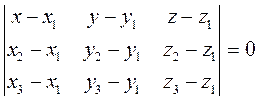. (24)
Example. Write an equation of the plane passing through the
; 
; 
.
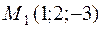By formula (24), we have
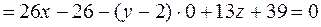or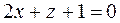 
.
The Angle between Planes
Consider the planes given by the equations
; 
,
which have normal vectors 
and 
. Using inner product, we find the cosine of the angle:
.
The condition for two planes to be parallel coincides with the condition for the normal vectors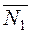 
and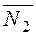 
to be collinear:
.
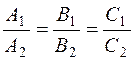The perpendicularity conditioin coincides with the perpendicularity condition for the vectors 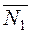and :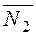
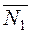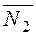( · )=0, i.e., A1A2+B1B2+C1C2=0.
Example 1. Show that the following planes are parallel or perpendicular:
.
The planes are perpendicular, because
.
Example 2. Write an equation of the plane passing through the point Ì0(–1;2; 4) and parallel to the plane 6x-7y+5z+11=0.
The normal vector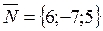 
is normal to the required plane also. We have
A(x–x0)+B(y–y0)+C(z–z0)=0,
6(x+1)–7(y–2)+5(z–4)=0; 6x–7y+5z=0.
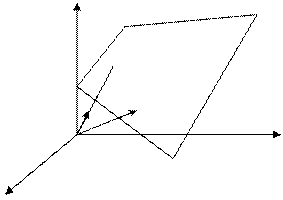The normal equation of a plane. Consider a plane. Let us draw the perpendicular ÎÐ from the origin to this plane. Let a,b, and g be the angels between this perpendicular and the coordinate axes x,y, and z, and let 
. It is required to write an equation of this plane.
z
P
M(x,y,z)
0 y
x
Take an arbitrary point M(x;y;z) in the plane and consider the radius-vector 
. The unit vector 
on the perpendicular ÎÐ has the coordinates
={cos α; cos b; cos g}.
For any point Ì in the plane, the projection of the vector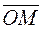 
on the unit vector equals ð:
.
Consider the scalar product
,
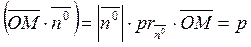or, in coordinate form,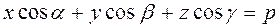 
.
Thus, we have obtained the normal equation of the plane:
. (25)
The normalizing factor. Consider the plane given by the general equation Ax+By+Cz+D=0.
It is required to reduce this equation to the normal form (25).
Definition. Number m is called the normalizing factor if the equation multiplied by it is normal.
To find the normalizing factor, we multiply the general equation of the plane by a number m term by term:
mAx+mBy+mCz+mD=0.
This equation is normal if the two normality conditions hold, i.e.,
1. (mA)2+(mB)2+(mC)2=1,
2. mD<0.
From the first condition, taking out m2 and extracting the square root, we find the normalizing factor.
.
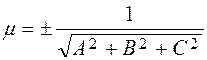The sign opposite to that of the free term D must be taken.
Date: 2015-01-02; view: 1606
| <== previous page | | | next page ==> |
| Analytic geometry in space. Vectors. Simple operations with vectors. The scalar, vector and mixed product of vectors | | | STRAIGHT LINES IN SPACE |