
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The Intersection of a Plane and a straight Line
Suppose given a plane Ax+By+Ñz+D=0
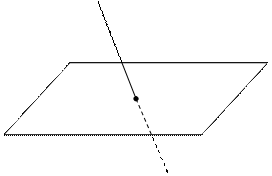 and a straight line
and a straight line 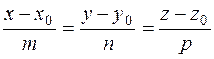 in space.
in space.
If the straight line and the plane do not intersect, then the parameter t1 does not exist. Suppose, that the line is parallel to the plane; then the vectors 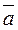 and
and 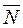 are perpendicular, i.e., or (
are perpendicular, i.e., or ( 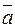 ·
· 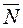 )=0, and Am+Bn+Cp=0. This means that the denominator vanishes.
)=0, and Am+Bn+Cp=0. This means that the denominator vanishes.
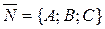

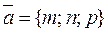
Thus, the parallelism condition for a straight line and a plane is
Am+Bn+Cp=0.
Suppose that the line is perpendicular to the plane; then the vectors 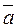 and
and 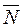 are collinear, i.e., their coordinates are proportional:
are collinear, i.e., their coordinates are proportional:
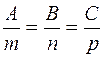 .
.
This is the perpendicularity condition for a straight line and a plane.
Example. Write the equation of a straight line perpendicular to the plane 2x-3y+4z+11=0 and passing through the intersection point of this plane with the line
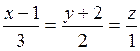 .
.
Let us reduce the canonical equation to the parametric form:
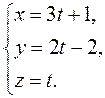
Substituting these expressions for the variables x,y, and z into the equation of the plane
6t+2–6t+6+4t+11=0.
Thus, 4t=–19, 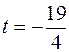 , and the intersection point of the line with the plane has the coordinates
, and the intersection point of the line with the plane has the coordinates
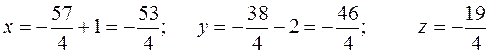 .
.
The normal vector to the plane is 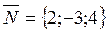 ; since the straight line is perpendicular to the plane, it follows that its direction vector is collinear to the normal vector, i.e.,
; since the straight line is perpendicular to the plane, it follows that its direction vector is collinear to the normal vector, i.e., 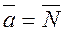 . Thus, the required straight line is determined by the equations
. Thus, the required straight line is determined by the equations
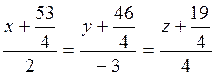 .
.
The angle between a plane and a straight line. Suppose that a plane in space is determined by its general equation
Ax+By+Ñz+D=0,
and a straight line is determined by its canonical equations
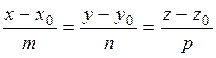 .
.
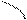  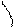   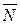 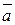
| Take the acute angle between the right line and its projection on the plane for the angle 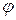 between the straight line and the plane. between the straight line and the plane.
|

Using the scalar product of vectors 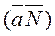 and the general scheme, we determine the angle
and the general scheme, we determine the angle 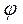 from the angle between the direction vector
from the angle between the direction vector  and the normal vector
and the normal vector
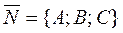 ;
; 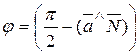 .
.
By the reduction formula, 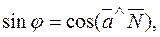 whence
whence
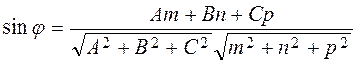 .
.
Definition. A directed interval (or an ordered pair of points) is called a vector.
 Â
Â
À 
Definition. A vector with coinciding endpoints is called the null vector.
Definition. The distance between the head and tail of a vector is called the length 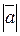 , or absolute value of this vector. It is denoted by
, or absolute value of this vector. It is denoted by 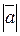 or
or  .
.
Definition. Vectors are collinear if they lie on the same straight line or on parallel lines.
A B C 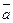



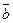

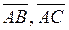 are collinear vectors,
are collinear vectors,
À1 Â1
 |
 ,
, 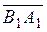 are collinear vectors.
are collinear vectors.
Definition. Vectors are coplanar if they lie in the same plane or in parallel planes.
Definition. Two vectors are said to be equal if they are collinear and have the same direction and length.
Date: 2015-01-02; view: 3418
| <== previous page | | | next page ==> |
| STRAIGHT LINES IN SPACE | | | Linear Operations on Vectors |