Analytic geometry in space. Vectors. Simple operations with vectors. The scalar, vector and mixed product of vectors

LECTURE PLAN

1. Planes

2. Vectors. Operations with vectors.

Planes

The general equation of a plane. Suppose given a vector 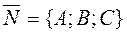perpendicular to a plane and a point in this plane. This vector is called a normal vector.

It is required to write an equation of the plane.

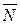
M(x,y,z)

M₀(x₀,y₀,z₀)

According to the general scheme, we take an arbitrary point M(x,y,z) in the plane.

Consider the vector 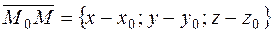. For any point in the plane, the vector 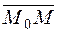is perpendicular to the normal vector .

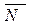Since , it follows that the scalar product vanishes: , or, in coordinate form,

, (*)

.

Denoting this numerical expression by D, we obtain

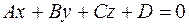. (23)

This is the general equation of a plane; the coefficients of A,B and C of x, y, and z are the coordinates of the normal vector .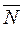

The three-intercept equation of a plane. Suppose given a plane not passing through the origin but intersecting the coordinate axes at points 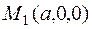, , and . Suppose also that the segments a,b, and c are known and it is required to write the equation of the plane from the intercepts. Let us write the general equation

.

The coefficients are not known yet, so we choose them so, that the plane cuts out the given segments a,b, and c on the coordinate axes.

Date: 2015-01-02; view: 1552