Line Pencils

Definition. A line pencil is the set of straight line passing through a given point.

Arbitrarily varying the coefficient k in the equation of a line passing through a point М0(х0,у0), we obtain equations of all straight lines passing through the point with coordinates х0, у0.

All these straight lines constitute the line pencil centered at М₀.

A line pencil can also be specified by two equations of lines from this pencil (which determine of these lines) the common point М₀(х₀, у₀) by the coordinates of its center.

Suppose given intersecting straight lines with general equations

,

.

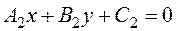Consider the equations

, (13)

where q₁ and q₂ undetermined multipliers, not both zero.

Let us prove that, for any q₁ and q₂, the straight line (13) passes through the point М₀ (х₀; у₀), which is the intersection point of the two given lines.

The coordinates of the point М₀ satisfy both equations

,

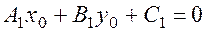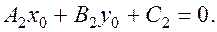
Consequently, the coordinates of М₀satisfy equation (13), i.e.,

.

Thus, the point М₀ belongs to the straight line (13) for any q₁ and q₂; but for particular values of q₁ and q₂, we obtain some straight line from the pencil.

In practice, it is more convenient to write an equation of a pencil with one parameter l:

.

Example. Draw a straight line through the intersection point of the lines х+у–3=0 and 2х–у+5=0 so that it passes through the point М(3;5).

Let us write the equation of the pencil of lines according to the formula. To find the required line, we must find the value of the parameter l:

We substitute the coordinates of the point М(3;5) into the equation of the pencil:

,

.

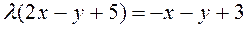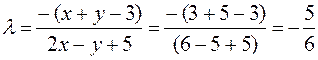Substituting l in to the equation of the pencil, we obtain the required equation:

;

.

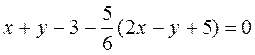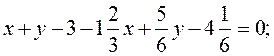
The Normal Equation of a Straight Line

The position of a straight line in the plane is completely determined by the distance from the line to the origin of coordinates, i.e., the length of the perpendicular from the origin to the fight line, and the unit normal vector

y

Т

α M

0 x

Let us construct an equation of a straight line from the length of the perpendicular р and its angle a with the x-axis.

To this end we take an arbitrary point М on the line and find the projection of the vector 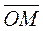on the unit normal vector .

The point М belongs to the given line if and only if

. (*)

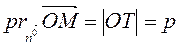In terms of inner product of vectors, we have

.

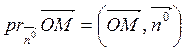Considering this product, we obtain

. (14)

Equation (14) is the normal equation of the line in vector form. To pass to coordinates, note that the projections of the unit normal vector are

,

where a is the angle between this vector and the axis ОX. Let the projections of the radius-vectors on the axes ОХ and ОУ are х and у, respectively. The inner product formula (14) implies

. (15)

This equation is called the normal equation of the straight line. It is clear from equation (15) that the “normality” conditions are

(1) 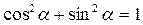(the sum of squared coefficients of х and у equals 1);

(2) –р<0 (the free element is negative).

Example. Which of the following equations are normal?

(a) 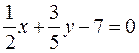, , 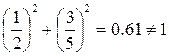this is not a normal equation;

(b) 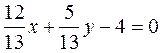, and –4<0, this is a normal equation;

(c) , 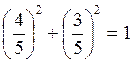but 2>0, this is not a normal equation.

A normalizing factor. Suppose given a general equation of a straight line given:

.

Definition. The normalizing factor is the number such that the equation multiplied by this number is normal.

Let us multiply the general equation of a straight line by number m:

.

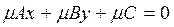By definition, if this equation is normal, then the two normality conditions hold:

; .

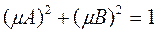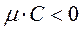Removing parentheses, we obtain

;

extracting the root, we see that the normalizing factor is

;

the sign of the fraction is opposite to that of the free element of the general equation.

Example. Reduce the equation 8х–6у+5=0 to the normal form.

We find the normalizing factor

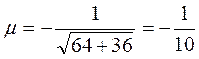
and multiply the equation by this factor term by term:

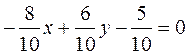or .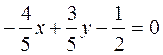

Date: 2015-01-02; view: 1257