
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The distance between two points. Let us find the distance between two points Ì1 and Ì2 in the plane.
 y
y
M2(x2;,y2)
d
M1(x1;y1)
0 x
Compose the vector 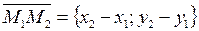 .
.
The length of this vector is defined by
 .
.
This is the distance between the two given points.
Example. Find the distance between the two points À(2;3) and Â(–4;11).
Using the above formula, we obtain
 .
.
Division of an interval in a given ratio. Suppose given an interval Ì1Ì2. Let us find the coordinates a of point Ì on the interval for which .
 Compose the vectors
Compose the vectors  and
and 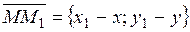 .
.
y
M2(x2,y2)
M(x,y)
M1(x1,y1)
0 x
This gives the x coordinate; y is found in a similar way:
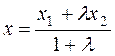 ;
; 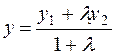 .
.
To obtain a formula for the midpoint of the interval, we take l=1:
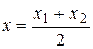 ;
;  .
.
Example. Given the two points Ì1(–2;4) and Ì2(6;2), find the midpoint of the interval Ì1, Ì2.
 Ì1
Ì1 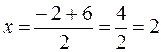 ,
,

Ì2 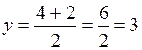 .
.
Lines and Their Equations
Definition. A line is the locus of points satisfying a characteristic condition of this line.
 |
y
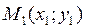


0 x
Definition. An equation of a line is a relation of the form
F  0,
0,
which holds for the coordinates of all points of the line, i.e.,
F(  ,
,
F( 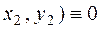 ,
,
F 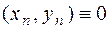 ,
,
. . . . . . . . . . . . . .
Straight Lines in the Plane
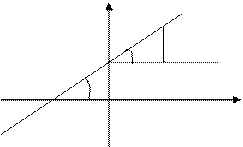
The equation of a straight line with a slope. Given a straight line, we denote the angle between this line and the x–axis by j and the interval cut out by the line on the x-axis by b.
 |
ó Ì(õ;ó)
 y-b
y-b
B j
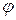 b N
b N
0 x
Definition. The slope tangent of the angle between a straight line and the x–axis is called the slope of the line and denoted by
k=tanj.
Suppose that k is the slope of a line and b is its y–intercept.
The equation of a straight line with a slope has the form

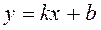 .
.
 The equation of a straight line with given slope passing through a given point. Suppose that a straight line passes through a point Ì0(x0,y0) and has slope k.
The equation of a straight line with given slope passing through a given point. Suppose that a straight line passes through a point Ì0(x0,y0) and has slope k.
y
M(x;y)
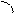 φ
φ
M0(x0;y0) N
 φ
φ
0 x
By analogy with the equation of a straight line with a slope consider the triangle Ì0MN; we have 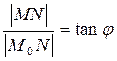 for any point Ì on the under
for any point Ì on the under
consideration or 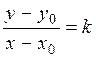 .
.
Thus, the required equation is
y – y0 = k(x–x0).
The equation of a straight line passing through two points. Suppose that a straight line passes through two points Ì1(õ1;ó1) and Ì2(õ2;ó2).
 y
y
M(x;y)
M2(x2;y2)
M1(x1;y1)
0 x
Take a point M(x,y) on the line and consider the vectors
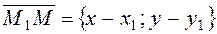 and
and  .
.
These two vectors 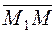 è
è 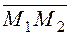 lie on the same straight line and are collinear.
lie on the same straight line and are collinear.
The collinearity condition is the proportionality of the perspective coordinates, i.e.,
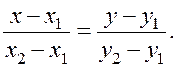 (10)
(10)
This is the equation of a straight line passing through the two given points.
Example. Write an equation of the straight line passing through the points Ì1(2;–5) and Ì2(3;2) and find k and b.
Using formula (10), we obtain
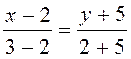 Þ 7x–14=y+5.
Þ 7x–14=y+5.
Thus the equation of the straight line is
y=7x–19,
and the slope and the y–intercept are
k=7, b= –19.
The general equation of a straight line and its analysis.
Definition. A first–order equation in variables x and y determines a straight line in the plane.
The general equation has the form
 ,
,
where À and  are called the coefficients of the variables.
1. If the free term is Ñ=0, then the equation has the form
 .
.
Since õ=0 and y=0 satisfy this equation, it follows that the straight line passes through the origin.
2. If the coefficient of õ is À=0, then the equation has the form
 or
or 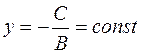 , i.e., the line is parallel to the x–axis.
, i.e., the line is parallel to the x–axis.
3. If the coefficient of y is B=0, then the equation has the form
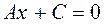 ,
,
and the line is parallel to the y–axis.
4. If À=Ñ=0, then the line
 ó=0 (or ó=0)
coincides with the x–axis.
5. If Â=Ñ=0, then the line
À õ=0 (or õ=0)
coincides with the y–axis.
2.7. 5. The two-intercept equation of a straight line. Suppose that a straight line intersects the coordinate axes in points M1(a;0) and Ì2(0;b)
ó 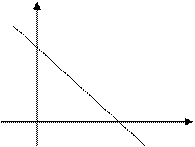
Ì2(0;b)
b
M1(a;0)
0 a x
Knowing the two points Ì1 and Ì2 through which the line passes, we can write the equation of the line in form (10):
 , or
, or  .
.
This is the two-intercept equation of the line.
Example. Reduce the equation 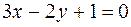 , to the two-intercept form.
, to the two-intercept form.
Take the variables to the left-hand side
 .
.
We have
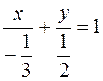 , where
, where  and
and 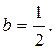
The angle between two straight lines. Parallel and perpendicular lines. Suppose given two straight lines with slopes 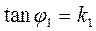 and
and  .
.
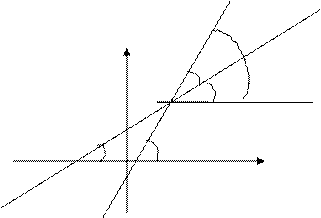 |
ó j=?
j1 j2
j1 j2
0 õ
It is seen from the figure that the angle between the lines equals j=j2–j1. Using the formula for the tangent of the difference between
two angels, we obtain
 .
.
Replacing the tangents by the slopes k1 and k2, we obtain the following formula for the tangent of the angle between two straight lines:
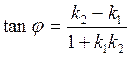 . (11)
. (11)
Formula (11) gives conditions for two lines to be parallel and perpendicular.
(1) Suppose that the right lines are parallel, i.e., the angle between them is  ; substituting it into formula (11), we obtain
; substituting it into formula (11), we obtain
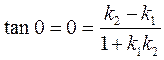 .
.
This fraction vanishes, if k2–k1=0.
Thus, two straight lines are parallel if and only if their slopes are equal:
k2=k1.
(2) Suppose that two straight lines are perpendicular; then the angle between them is  . Substituting it in (11), we obtain
. Substituting it in (11), we obtain
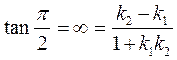 .
.
This fraction equals infinity when the denominator vanishes:
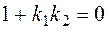 .
.
Consequently, the condition for two straight lines to be perpendicular is
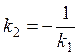 .
.
Example. Write equations of the straight lines passing through the point Ì0(1;1) and parallel and perpendicular to the line 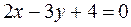 .
.
Let us write the equation of the given line in the form y=kx+b:
 , or
, or 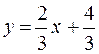 ;
; 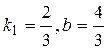 .
.
To compose an equation of a straight line, we use the formula
 . (*)
. (*)
Since the required line must be parallel to the required one, it follows that
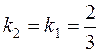 .
.
Substituting this into equation (*), we obtain
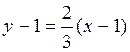 , or
, or 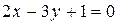 .
.
The perpendicularity condition gives the slope:
 .
.
The equation of the required line is
 ;
; 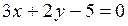 .
.
The mutual arrangement of two straight lines. Given equations of two straight lines
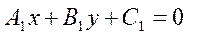 and
and 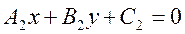 .
.
Determine conditions on the coefficient, for these right lines to intersect, be parallel, or coincide.
1. To determine the mutual arrangement of lines, we must analyze the system of equations

If the lines intersect, then this system has a unique solution, and its principal determinant is nonzero:
 ;
; 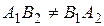 ;
;
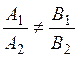 . (12)
. (12)
Thus, if the straight lines intersect, then the coefficients must not be proportional.
2. Suppose that the straight lines are parallel, i.e., they have no common points, and the system of equations has no solution; then the principal determinant vanishes, and the auxiliary determinants are nonzero:
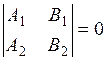 ;
;  ;
;
 ;
;
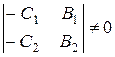 ;
;  ;
; 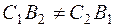 ;
; 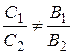 ;
;
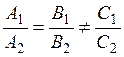 . (12΄)
. (12΄)
This is the parallelis condition.
3. When the straight lines coincide, i.e., have many common points, the system of equations has infinitely many solutions. In this case, the auxiliary and principal determinants are zero:
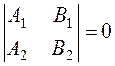 ;
;  ;
;
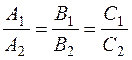 . (12΄΄)
. (12΄΄)
This is the condition for straight lines to coincide.
Example. 1. Concider the straight lines given by

According to formula (12), we have  , which means that these lines intersect.
, which means that these lines intersect.
2. Consider the straight lines given by
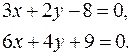
According to formula (12΄), we have 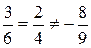 , and the lines are parallel.
, and the lines are parallel.
3. Consider the straight lines given by

According to formula (12΄΄) we have 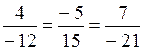 , and the lines coincide.
, and the lines coincide.
Date: 2015-01-02; view: 3401
| <== previous page | | | next page ==> |
| LECTURE 3. | | | Line Pencils |