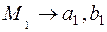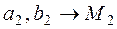LECTURE 3.

The simplest problem of analytic geometry. Equations of a straight line on a plane.

LECTURE PLAN:

1. The simplest problem of analytic geometry

2. Equations of a straight line on a plane

Analytic Geometry in the Plane

Consider the Cartesian rectangular coordinate system in the plane. Taking the projection of any point М₁ on the x and y coordinate we obtain two numbers x=a₁ and y=b₁. Take two numbers a₂ and b₂ plot a₂ on the x-axis and b₂ on the y-axis . Having drawn two straight lines parallel to the coordinate axes through these points we find obtain a point M₂ in their intersection.

		x

0

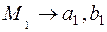
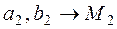
Thus, there is a one–to–one correspondence between points in the plane and pairs of numbers.

Date: 2015-01-02; view: 1268