
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Matrices and Operations on Them
Definition. A matrix of size 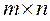 is a table written in parentheses or between two pairs of parallel lines:
is a table written in parentheses or between two pairs of parallel lines:
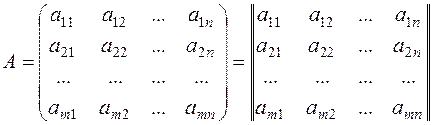 ,
,
m is the number of rows, n is the number of columns, and àij is an element of the matrix.
If m=n, then the matrix is square.
A null-matrix is a matrix À, in which all elements are zero:
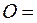
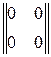 ;
; 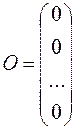 .
.
Definition. A square matrix À is said to be diagonal if its main diagonal may contain nonzero elements, but all nondiagonal elements are zero:
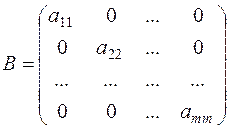 .
.
Definition. The identity matrix is the diagonal matrix with ones on the diagonal:
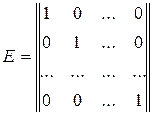 .
.
Definition. Matrices of the same size are equal if their respective elements are equal.
Two matrices of the same size can be added (elementwise):
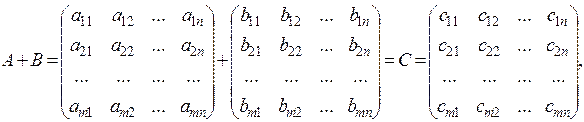
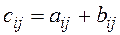 .
.
Any matrix can be multiplied by any number all elements of the matrix should be multiplied by this number):
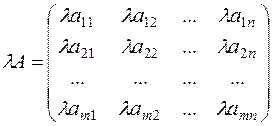 .
.
Subtraction is defined as
À–Â=À+(–1)Â.
Two matrices can be multiplied only if the number of columns in the first matrix equals the number of rows in the second matrix. An 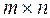 matrix is multiplied by an
matrix is multiplied by an 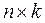 matrix as follows:
matrix as follows:
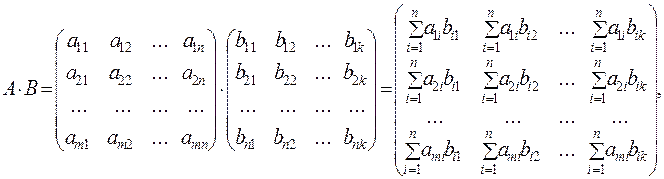
We obtain a matrix of size 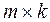 .
.
Multiplication of matrices is not commutative, and sometimes even impossible:
ÀÂ 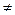 ÂÀ.
ÂÀ.
Date: 2015-01-02; view: 1732
| <== previous page | | | next page ==> |
| Cramer’s Rule | | | The Gauss-Jordan Method |