Cramer’s Rule

To solve system (3), we multiply the first equation by А₁₁, the second by А_21, etc., the last equation is multiplied by А_n1. Then, we sum the equations and collect similar terms:

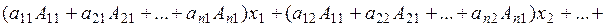
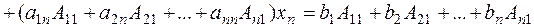
Consider the nth-order determinant composed of the coefficients of system (3):

. (4)

The coefficient of х₁ is the sum of the products of the element of the first column and their algebraic complements. According to property 9, it equals determinant (4).

The coefficients of the unknowns 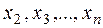are the products of the elements of the second, third, …, nth columns by the algebraic complements of the elements of the first column; consequently, they equal zero by property 10.

The right-hand side is the product of the free terms and the algebraic complements of the elements of the first column; consequently, it equals the determinant (4) in which the first column is replaced by the column of free terms:

, .

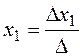Expressions for the other unknowns are obtained in a similar way: we multiply system (3) by the algebraic complements of the n corresponding columns

, , (5)

where 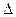is the principal determinant of the system and the 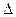х_i are the auxiliary determinants obtained from the principal one by substituting the free term column for the ith columns.

Example. Solve the system of equations

Let us evaluate the principal determinant of the system:

.

To obtain zeros in the first row, we leave the third column unchanged; multiply it by –2 and add to the first column; then multiply it by 3 and add to the second column.

Let us calculate the auxiliary determinants. х₁ is derived from  by replacing the first column by the free terms:

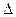х₂ is derived from 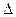 by replacing the second column by the free terms:

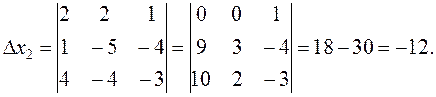
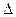х₃ is derived from 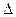by replacing the third column by the free terms. Zeroes are obtained in the third row by adding the second column multiplied by –4 and 4 to the first and third columns, respectively:

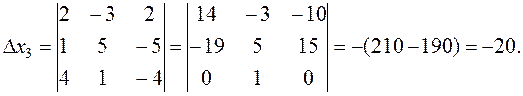
By Cramer's rule (5) we obtain

; ;

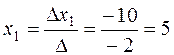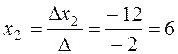1. In (5), the principal determinant must be different from zero. In this case, system (3) has a unique solution.

2. If 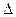=0 and one of the auxiliary determinants does not equal zero ( 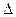x 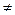0), then the system has no solutions at school, we would say that division by zero is not allowed.

3. If 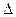=0 and all of the auxiliary determinants equal zero ( 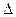x_i=0), then the system has infinitely many solutions.

Date: 2015-01-02; view: 1377