Systems of Linear Equations

Consider system of m linear equations with n unknowns:

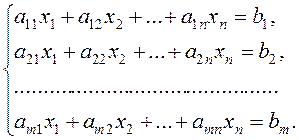
(2)

Definition. The numbers are called a solution of system (2) if substituting them into the equations, we obtain true equalities.

Definition. A system of equations (2) is said to be consistent if it has at least one solution, and it is said to be inconsistent if it has no solutions.

Definition. A system is called determined if it has a unique solution, and it is called undetermined if it has many solutions.

For example, the system of equations

has no solutions, i.e., it is inconsistent, because its left-hand sides are equal, while the right-hand sides are different.

is consistent, but undetermined, because it has infinitely many solutions. Reducing the second equation by 3, we obtain two identical equations.

Consider the following system of n linear equations with n unknowns

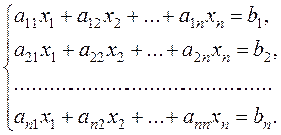(3)

It is required to find a solution 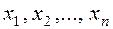of system (3), expressed in terms of the coefficients 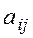and the free terms , where (from 1 to n).

Date: 2015-01-02; view: 1247