Determinants and their properties. Matrix. Operations with matrices. The inverse matrix. Systems of linear equations

LECTURE PLAN:

1. Determinants and their properties

2. Мatrices

3. Nonsingular matrices

4. Systems of linear equations

Determinants and their properties

Determinants of second and third order

Consider the system of two linear algebraic equations in two variables

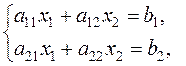(1)

where a₁₁,a₁₂,a₂₁, and a₂₂ are coefficients, b₁ and b₂ are right-hand sides, and x₁ and x₂ are unknowns.

Let us solve this system by the school method of algebraic addition, namely, multiply the first and second equations by а₂₂ and – a₁₂ , respectively, and sum the results. The coefficient of х₂ will vanish. The remaining unknown, х₁, is found as follows:

x₁(a₁₁a₂₂–a₁₂a₂₁)=b₁a₂₂–a₁₂b₂,

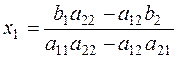
In a similar manner, multiplying the first equation of the system by – а₂₁, the second by а₁₁ , and summing the resulting equations term by term, we obtain

,

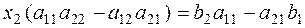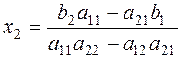
Definition. The number

is called a determinant of second order.

The numbers a₁₁,a₁₂,a₂₁ and a₂₂ are called the elements of the determinant.

The second-order determinant is equal to the product of the elements of the main diagonal minus the product of the elements of the secondary diagonal.

Example . Find the determinants

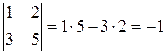
The unknowns х₁ and х₂ of the linear system (1) are determined by the formulas

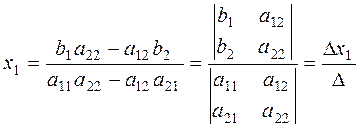
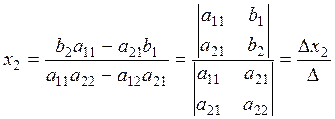
The determinant is called the principal determinant of the system; it is formed by the coefficients of the unknowns. 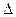x₁ and 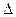x₂ are auxiliary determinants; they are obtained by replacing the elements of the first and second columns by the free terms of system (1).

Example.

,

, ,

, .

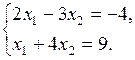
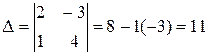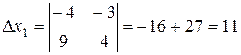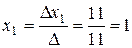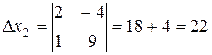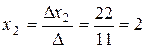A third-order determinant is the number

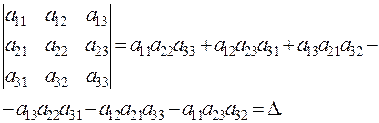
The simplest method for calculating a third-order determinant is the triangle rule.

The main diagonal of the determinant is the line containing the elements a₁₁,a₂₂ and a₃₃.

The secondary diagonal is the line containing the elements a₁₃,a₂₂ and a₃₁.

The products of the main diagonal elements and of the elements contained in the triangles shown below are summed with the plus sign:

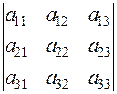
The products of the secondary diagonal elements and of the elements contained in the triangle shown below are summed with the minus sign:

.

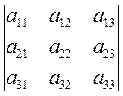Another method for calculating a third-order determinant is as follows. We write the first columns on the right of the determinant, and sum the products of the elements of the main diagonal and of the two parallel diagonals with the plus sign. Then we add the products of the elements of the secondary diagonal and of the two parallel diagonals with the minus sign

+ + +

– – –

As a result, we obtain the determinant.

Example. Calculate the determinant by the triangle rule:

.

The determinant of order n is the expression

.

An nth-order determinant contains n² elements.

The subscript, i, indicates the number of the row and the second subscript j, indicates the number of the column containing the element а_ij.

Properties of determinants. All determinants of any order have the same properties. For simplicity, we give only properties of third-order determinants.

1. The interchange of rows and columns in a determinant does not change its value:

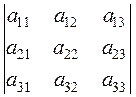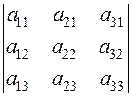= (the transposed determinant).

2. The interchange of two rows (columns) in a determinant changes only the sign of the determinant:

.

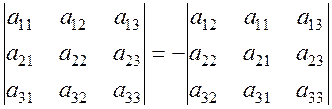3. If all elements of any lines (a row or a column) are zero, then the determinant is equal to zero:

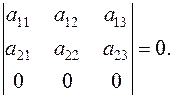
The proof follows from the triangle rule.

4. A determinant containing two equal lines is equal to zero:

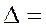
=0.

5. The common multiplier of all elements of a line can be factored out:

.

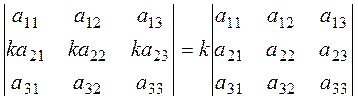6. A determinant containing two proportional lines, is equal to zero:

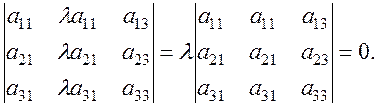
7. If each element of some line is the sum of two terms, then such a determinant equals the sum of two determinants, which contain these terms instead of the elements of the lines.

.

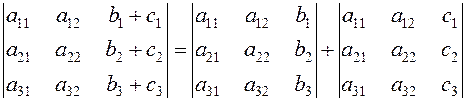8. A determinant does not change under the replacement of any line by the sum of this line and any parallel line multiplied by some number.

Algebraic complements and minors.

Definition. The minor of an element а_ij is the determinant of order lower by one consisting of the elements that remain after the deletion of the ith-series and jth-column, which intersect in a_ij.

For example, the minor of the element a₃₂ is

;

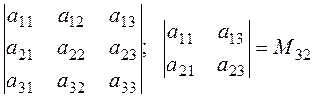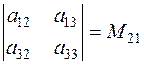is the minor of .

Definition. The algebraic complement of an element а_ij is the minor of a_ij multiplied by -1 raised to the proper equal to the sum of the numbers of the row and the column intersecting in the given element:

.

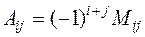9. A determinant equals the sum of products of all elements of any lines and the corresponding algebraic complements.

.

For a kth order determinant, we can write property 9 in the form of expansion along the kth-column:

.

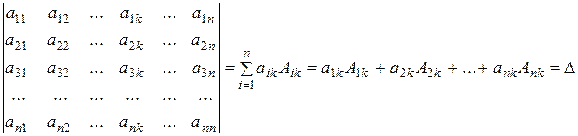10. The sum of the products of the elements of any line and the algebraic complements of the corresponding elements of a parallel line equals zero:

=

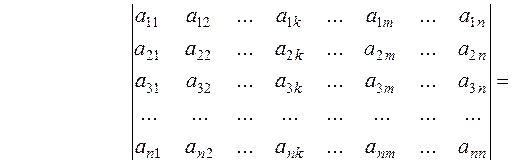
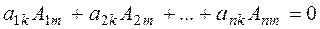
Examples. Let us expand the following determinant along the third row:

Date: 2015-01-02; view: 1867