A Real Life Example

A group travelled on a bus, at $3 per child and $3.20 per adult for a total of $118.40.

They took the train back at $3.50 per child and $3.60 per adult for a total of $135.20.

How many children, and how many adults?

First, let us set up the matrices (be careful to get the rows and columns correct!):

This is just like the example above:

XA = B

So to solve it we need the inverse of "A":

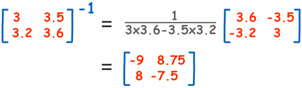
Now we have the inverse we can solve using:

X = BA^-1

There were 16 children and 22 adults!

The answer almost appears like magic. But it is based on good mathematics.

Calculations like that (but using much larger matrices) help Engineers design buildings, are used in video games and computer animations to make things look 3-dimensional, and many other places.

It is also a way to solve Systems of Linear Equations.

The calculations are done by computer, but the people must understand the formulas.

Order is Important

Say that you are trying to find "X" in this case:

AX = B

This is different to the example above! X is now after A.

With Matrices the order of multiplication usually changes the answer. Do not assume that AB = BA, it is almost never true.

So how do we solve this one? Using the same method, but put A^-1 in front:

A^-1AX = A^-1B

And we know that A^-1A= I, so:

IX = A^-1B

We can remove I:

X = A^-1B

And we have our answer (assuming we can calculate A^-1)

Why don't we try our example from above, but with the data set up this way around.(Yes, you can do this, just be careful how you set it up.)

This is what it looks like as AX = B:

It looks so neat! I think I prefer it like this.

Also note how the rows and columns are swapped over ("Transposed")
compared to the previous example.

To solve it we need the inverse of "A":

It is like the Inverse we got before, but
Transposed (rows and columns swapped over).

Now we can solve using:

X = A^-1B

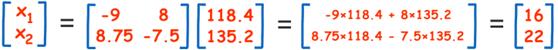
Same answer: 16 children and 22 adults.

So, Matrices are powerful things, but they do need to be set up correctly!

Date: 2015-12-11; view: 1443