Inverse of a Matrix

Please read our Introduction to Matrices first.

What is the Inverse of a Matrix?

The Inverse of a Matrix is the same idea as the reciprocal of a number:

Reciprocal of a Number

But we don't write ¹/_A (because we don't divide by a Matrix!), instead we write A^-1 for the inverse:

(In fact ¹/₈ can also be written as 8^-1)

And there are other similarities:

When you multiply a number by its reciprocal you get 1

8 × (¹/₈) = 1

When you multiply a Matrix by its Inverse you get theIdentity Matrix (which is like "1" for Matrices):

A × A^-1 = I

It also works when the inverse comes first: (¹/₈) × 8 = 1 and A^-1 × A = I

Identity Matrix

Note: the "Identity Matrix" is the matrix equivalent of the number "1":

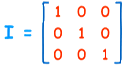
A 3x3 Identity Matrix

• It is "square" (has same number of rows as columns),
• It has 1s on the diagonal and 0s everywhere else.
• It's symbol is the capital letter I.

The Identity Matrix can be 2×2 in size, or 3×3, 4×4, etc ...

Definition

So we have a definition of a Matrix Inverse ...

The Inverse of A is A^-1 only when:

A × A^-1 = A^-1 × A = I

Sometimes there is no Inverse at all.

X2 Matrix

OK, how do we calculate the Inverse?

Well, for a 2x2 Matrix the Inverse is:

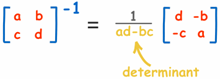
In other words: swap the positions of a and d, put negatives in front of b and c, and divide everything by the determinant (ad-bc).

Let us try an example:

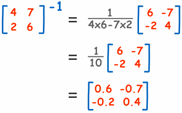
How do we know this is the right answer?

Remember it must be true that: A × A^-1 = I

So, let us check to see what happens when we multiply the matrix by its inverse:

And, hey!, we end up with the Identity Matrix! So it must be right.

It should also be true that: A^-1 × A = I

Why don't you have a go at multiplying these? See if you also get the Identity Matrix:

Why Would We Want an Inverse?

Because with Matrices we don't divide! Seriously, there is no concept of dividing by a Matrix.

But we can multiply by an Inverse, which achieves the same thing.

Imagine you couldn't divide by numbers, and someone asked "How do I share 10 apples with 2 people?"

But you could take the reciprocal of 2 (which is 0.5), so you could answer:

10 × 0.5 = 5

They get 5 apples each

The same thing can be done with Matrices:

Say that you know Matrix A and B, and want to find Matrix X:

XA = B

It would be nice to divide both sides by A (to get X=B/A), but remember we can't divide.

But what if we multiply both sides by A^-1 ?

XAA^-1 = BA^-1

And we know that AA^-1 = I, so:

XI = BA^-1

We can remove I (for the same reason we could remove "1" from 1x = ab for numbers):

X = BA^-1

And we have our answer (assuming we can calculate A^-1)

In that example we were very careful to get the multiplications correct, because with Matrices the order of multiplication matters. AB is almost never equal to BA.

Date: 2015-12-11; view: 1391