
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The Inverse May Not Exist
First of all, to have an Inverse the Matrix must be "Square" (same number of rows and columns).
But also the determinant cannot be zero (or you would end up dividing by zero). How about this:

24-24? That equals 0, and 1/0 is undefined.
We cannot go any further! This Matrix has no Inverse.
Such a Matrix is called "Singular", which only happens when the determinant is zero.
And it makes sense ... look at the numbers: the second row is just double the first row, and does not add any new information.
Imagine in our example above that the prices on the train were exactly, say, 50% higher ... we wouldn't be any closer to figuring out how many adults and children ... we need something different.
And the determinant neatly works this out.
Linear space
A linear space is a basic structure in incidence geometry. A linear space consists of a set of elements called points, and a set of elements called lines. Each line is a distinct subset of of the points. The points in a line are said to be incident with the line. Any two lines may have no more than one point in common. Intuitively, this rule can be visualized as two straight lines, which never intersect more than once.
Linear spaces can be seen as a generalization of projective and affine planes, and more broadly, of 2-  block designs, where the requirement that every block contains the same number of points is dropped and the essential structural characteristic is that 2 points are incident with exactly 1 line.
block designs, where the requirement that every block contains the same number of points is dropped and the essential structural characteristic is that 2 points are incident with exactly 1 line.
The term linear space was coined by Libois in 1964, though many results about linear spaces are much older.
Definition
Let L = (P, G, I) be an incidence structure, for which the elements of P are called points and the elements of G are called lines. L is a linear space if the following three axioms hold:
· (L1) two points are incident with exactly one line.
· (L2) every line is incident to at least two points.
· (L3) L contains at least two lines.
Some authors drop (L3) when defining linear spaces. In such a situation the linear spaces complying to (L3) are considered as nontrivial and those who don't as trivial.
8. Euclidean plane
The regular Euclidean plane with its points and lines constitutes a linear space, moreover all affine and projective spaces are linear spaces as well.
The table below shows all possible nontrivial linear spaces of five points. Because any two points are always incident with one line, the lines being incident with only two points are not drawn, by convention. The trivial case is simply a line through five points.
In the first illustration, the ten lines connecting the ten pairs of points are not drawn. In the second illustration, seven lines connecting seven pairs of points are not drawn.

| 
| 
| 
|
| 10 lines | 8 lines | 6 lines | 5 lines |
A linear space of n points containg a line being incident with n − 1 points is called a near pencil. (See pencil)

|
| near pencil with 10 points |
Dot Product
These are vectors:

They can be multiplied using the "Dot Product" (also see Cross Product).
Calculating
You can calculate the Dot Product of two vectors this way:

| a · b = |a| × |b| × cos(θ) Note: |a| means the magnitude (length) of vector a (multiply the length of a times the length of b, then multiply by the cosine of the angle between a and b) |
OR you can calculate it this way:

| a · b = ax × bx + ay × by (multiply the x's, multiply the y's, then add) |
They both work!
Example: Calculate the dot product of vectors a and b:

a · b = |a| × |b| × cos(θ)
a · b = 10 × 13 × cos(59.5°)
a · b = 10 × 13 × 0.5075...
a · b = 65.98... = 66 (rounded)
a · b = ax × bx + ay × by
a · b = -6 × 5 + 8 × 12
a · b = -30 + 96
a · b = 66
Both methods came up with the same result (after rounding)
Also note that we used minus 6 for ax (it is heading in the negative x-direction)
Cross Product
These are vectors:

They can be multiplied using the "Cross Product" (also see Dot Product).
The Cross Product of two vectors is another vector that is at right angles to both.
And it all happens in 3 dimensions!
Calculating
You can calculate the Cross Product this way:

| a × b = |a| |b| sin(θ) n |a| is the magnitude (length) of vector a |b| is the magnitude (length) of vector b θ is the angle between a and b n is the unit vector at right angles to both a and b So the length is: the length of a times the length of b times the sine of the angle between a and b, Then you multiply by the vector n to make sure it heads in the right direction. |
OR you can calculate it this way:

| When a and b start at the origin point (0,0,0), the Cross Product will end at:
|
They both work!
Example: What is the cross product of a = (2,3,4) and b = (5,6,7)
· cx = aybz - azby = 3×7 - 4×6 = -3
· cy = azbx - axbz = 4×5 - 2×7 = 6
· cz = axby - aybx = 2×6 - 3×5 = -3
Answer: a × b = (-3,6,-3)
Dot Product
The Cross Product gives a vector answer, and is sometimes called the "vector product"
But there is also the Dot Product which gives a scalar (ordinary number) as an answer.
11. Number sequence and its limit.
Number sequence is an infinite set of numbers one after another in a particular order and constructed according to a specific law, by which the function is defined as an integer argument, An. Ie
A number is called a limit order if for any A there exists a number N, such that the inequality?
Number sequence can have more than one limit. The sequence has a limit, called convergent.
a stationary sequence is a random sequence whose joint probability distribution is invariant over time. If a random sequence X j is stationary then the following holds:

where F is the joint cumulative distribution function of the random variables in the subscript.
If a sequence is stationary then it is wide-sense stationary.
If a sequence is stationary then it has a constant mean (which may not be finite):

A sequence is bounded below if all its terms are greater than or equal to a number, K, which is called the lower bound of the sequence.
an ≥ k
The greatest lower bound is called the infimum.
Bounded Sequence
A sequence is bounded if it is bounded above and below, that is to say, if there is a number, k, less than or equal to all the terms of sequence and another number, K', greater than or equal to all the terms of the sequence. Therefore, all the terms in the sequence are between k andK'.
k ≤ an≤ K'
Examples
Study the following sequences and determine if they are bounded.
1 
3, 4/3, 1, 6/7,...
As the sequence is decreasing, 3 is an upper bound and the supremum.
a1000= 0.5012506253127.
a1000 000 = 0.5000012500006.
The limit is 0.5.
0.5 is a lower bound and the infimum.
Thus, the sequence is bounded.
1/2 < an ≤ 3
Infinite large
A sequence  is called infinite large if it approaches infinity as number n tends to infinity.
is called infinite large if it approaches infinity as number n tends to infinity.
A formal definition is the following:
A sequence  is called infinite large if for any arbitrary large and positive number is called infinite large if for any arbitrary large and positive number 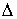 there exists a natural numberNsuch that there exists a natural numberNsuch that
 for eachn > N.
for eachn > N.
|
This statement is written symbolically just in the same manner as above:
 ,
,
 ,
,
 as
as  .
.
The symbolical notations
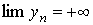 and
and 
mean that the terms of infinite large sequence  are, respectively, all positive or all negative at least starting from a sufficiently large number n.
are, respectively, all positive or all negative at least starting from a sufficiently large number n.
| Graphic Illustrations | 
|
The absolute values of terms xn are greater than any arbitrary large number D>0, starting from the term xN+1:


13. infiniresimal
| Property 1 | proof |
| The product of an infinitesimal sequence and a bounded sequence is an infinitesimal sequence. |
Explanation: The absolute values of the terms of a bounded sequence  are restricted by a finite positive number M, that is,
are restricted by a finite positive number M, that is,

for each natural n.
If  is an infinitesimal variable then
is an infinitesimal variable then
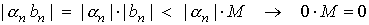 .
.
| Property 2 | proof | 
|
| The sum of two infinitesimal sequences is an infinitesimal sequence |
Explanation: If  and
and  are infinitesimal sequences then
are infinitesimal sequences then
 .
.
| Property 2 Corollary | proof | 
|
| The sum of any finite number of infinitesimal sequences is an infinitesimal sequence |
Explanation: An idea of a proof is shown in the drawing below, namely, the sum of two infinitesimals is an infinitesimal, the sum of which and a third infinitesimal is also infinitesimal, etc.

| Property 3 | proof | 
|
| The sequence inverse of an infinitesimal sequence is infinite large; and vice versa: The sequence inverse of an infinite large sequence is infinitesimal. |
Explanation: To verify these propositions, divide number one by 1000, 1000000, 1000000000, and so on. Then divide number one by 0.001, 0.000001, 0.000000001, and so on.
14. convergent
Date: 2015-12-11; view: 1285
| <== previous page | | | next page ==> |
| A Real Life Example | | | Finish up the sentences by adding one of the fragments. |