
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Calculating the Determinant
First of all the matrix must be square (i.e. have the same number of rows as columns). Then it is just a matter of basic arithmetic. Here is how:
For a 2×2 Matrix
For a 2×2 matrix (2 rows and 2 columns):
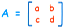
The determinant is:
|A| = ad – bc "The determinant of A equals a times d minus b times c"
It is easy to remember when you think of a cross:
| 
|
Example:

| |B| | = 4×8 - 6×3 |
| = 32-18 | |
| = 14 |
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):

The determinant is:
|A| = a(ei - fh) - b(di - fg) + c(dh - eg)
"The determinant of A equals ... etc"
It may look complicated, butthere is a pattern:

To work out the determinant of a 3×3 matrix:
- Multiply a by the determinant of the 2×2 matrix that isnot in a's row or column.
- Likewise for b, and for c
- Add them up, but remember that b has a negative sign!
As a formula (remember the vertical bars || mean "determinant of"):
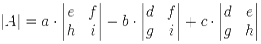
"The determinant of A equals a times the determinant of ... etc"
Example:
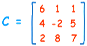
| |C| | = 6×(-2×7 - 5×8) - 1×(4×7 - 5×2) + 1×(4×8 - -2×2) |
| = 6×(-54) - 1×(18) + 1×(36) | |
| = -306 |
For 4×4 Matrices and Higher
The pattern continues for 4×4 matrices:
- plus a times the determinant of the matrix that isnot in a's row or column,
- minus b times the determinant of the matrix that isnot in b's row or column,
- plus c times the determinant of the matrix that isnot in c's row or column,
- minus d times the determinant of the matrix that isnot in d's row or column,

As a formula:
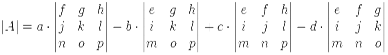
Notice the + - + - pattern (+a... -b... +c... -d...). This is important to remember.
The pattern continues for 5×5 matrices and higher.
Not The Only Way
This method of calculation is called the "Laplace expansion" ... I like it because the pattern is easy to remember. But there are other methods (just so you know).
Summary
· For a 2×2 matrix the determinant isad - bc
· For a 3×3 matrix multiply a by the determinant of the 2×2 matrix that isnot in a's row or column, likewise for b and c, but remember that b has a negative sign!
· The pattern continues for larger matrices: multiply aby the determinant of the matrix that isnot in a's row or column, continue like this across the whole row, but remember the + - + - pattern.
5. Systems of Linear Equations
A linear equation in the variables x1, x2, . . ., xn is an equation that can be written in the form a1x1 +a2x2 +. . . anxn = b, where a1, . . ., an are the coefficients. A system of linear equations (or a linear system) is a collection of one or more linear equations involving the same variables. A solution of a linear system is a list of numbers that makes each equation a true statement. The set of all possible solutions is called the solution set of the linear system. Two linear systems are called equivalent if they have the same solution set. A linear system is said to be consistent, if it has either one solution or infinitely many solutions. A system is inconsistent if it has no solutions.
Cramer’s Rule
A method for solving a linear system of equations using determinants. Cramer’s rule may only be used when the system is square and the coefficient matrix isinvertible.


Date: 2015-12-11; view: 1461
| <== previous page | | | next page ==> |
| Linearly Dependent Vectors | | | Inverse of a Matrix |