Linearly Dependent Vectors

Vectors are linearly dependent if there is a linear combination of them that equals the zero vector, without the coefficients of the linear combination being zero.

Properties

1.If several vectors are linearly dependent, then at least one of them can be expressed as a linear combination of the others.

If a vector is a linear combination of others, then all the vectors are linearly dependent.

2.Two vectors in the plane are linearly dependent if, and only if they are parallel.

3.Two vectors in the plane = (u₁, u₂) and = (v₁, v₂) are linearly dependent if their components are proportional.

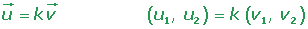
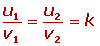
Linearly Independent Vectors

Several vectors are linearly independent if none of them can be expressed as a linear combination of the others.

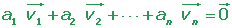
a₁ = a₂ = ··· = a_n = 0

Examples

Determine if the vectors are linearly dependent or independent:

= (3, 1) and = (2, 3)

Linearly independent

Determine if the vectors are linearly dependent or independent:

= (x − 1, 3) and = (x + 1, 5)

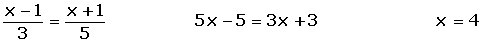
Are vectors are linearly dependent for x = 4.

Determine if the vectors are linearly dependent or independent:

= (5, 3 − x ) and = (x + 9, 3x + 1)

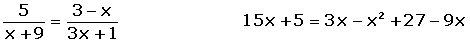
They are linearly dependent for x = 1 and x = −22

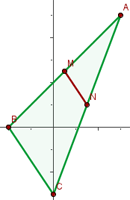
Check that the line segment joining the midpoints of sides AB and AC of the triangle: A (3, 5), B (−2, 0), C (0, −3) are parallel to the side BC and equal to its half.

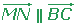
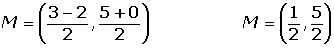
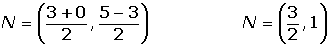
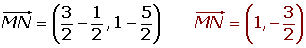
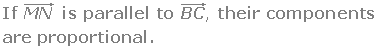
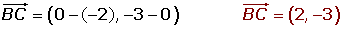
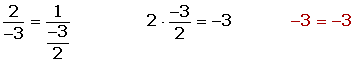
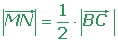
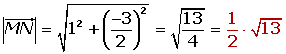
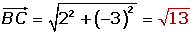
Determinant of a Matrix

A Matrix is an array of numbers:

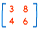
A Matrix
(This one has 2 Rows and 2 Columns)

Determinant

The determinant of a matrix is a special number that can be calculated from the matrix. It tells us things about the matrix that are useful in systems of linear equations, in calculus and more.

The symbol for determinant is two vertical lines either side.

Example:

|A| means the determinant of the matrix A

Date: 2015-12-11; view: 969