C. PERPENDICULAR PLANES

Rule:If a plane contains a line perpendicular to another plane then it is perpendicular to that plane.

Every line on any of two parallel planes is parallel to the other plane. So, if a plane is perpendicular to another plane, it intersects the plane.

Let α and β be two planes so that α ^ β. Then in α there can be found a line m perpendicular to β. Then line m is perpendicular to the intersection of α and β because this line lies in β.

Moreover in α through every point there can be drawn a line parallel to m. Since m is perpendicular to β all these lines are perpendicular to β. Therefore, it can be concluded that in α through every point there can be drawn a line perpendicular

to β.

Theorems:

1.If one of two planes is perpendicular to the other then the other is perpendicular to the first one too.

2.Any plane perpendicular to one of two parallel planes is perpendicular to the other.

3.If a line is perpendicular to a plane and parallel to another plane, these planes are perpendicular.

Proofs:

1.Let α be a plane perpendicular to a plane β.

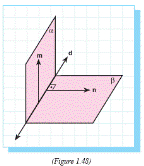
Then in α there is a line m so that m ⊥ β (Figure 1.48).

Let d be the intersection of α and β.

Since m ⊥ β, m intersects β.

Since m is in α, m intersects β at a point which is on d.

So m and d are two intersecting lines. (Figure 1.48)

Let n be any line in β which is perpendicular to d.

Since m ⊥ β, m ⊥ n. So n is perpendicular to two intersecting lines in β which are m and d.

So n ⊥ α. Hence β ⊥ α.

2.Let α and β be two parallel planes and λ be a plane perpendicular to α.

Then in λ there is a line perpendicular to α.

This line will be also perpendicular to β .

So λ ⊥ β.

3.In the plane parallel to the line, there will be a line parallel to the given line and this line will be perpendicular to the other plane.

So the planes are perpendicular

Example 35:Show that if two intersecting planes α and β are perpendicular to a given plane λ then intersection line of α and β is perpendicular to λ.

Solution: Let α and λ intersect along line m.

Since α ^ λ, in α there can be found a line d perpendicular to λ, and since β ^ λ, in λ there

can be found a line k perpendicular to λ.

If two lines are perpendicular to the same plane, they are parallel. So d and k are parallel.

Since d and k are two parallel lines in two intersecting planes, they are parallel to the intersection line of these planes.

So m // d and m // k.

So m ⊥ λ too.

Example 36:Line m is parallel to plane α. Show that there can be drawn one and only one plane containing m and perpendicular to α.

Solution:Let us prove that this plane can be drawn.

Let A be a point on m.

Through A there can be drawn line d perpendicular to α.

Then m and d determine a plane β. β contains line d which is perpendicular to α.

So β ⊥ α.

Now let us prove that this plane is unique.

Assume that there are planes β₁ and β₂ passing

through m and perpendicular to α.

Let A be a point on m.

Since A is in β₁ and β₂ we can draw two lines which are in β₁ and β₂ and perpendicular to α.

However we proved that through a given point there can be drawn only one line perpendicular to α.

So d₁ and d₂ will be same line.

Then β₁ and β₂ will have two common lines which are m and d₁.

So they are coincident.

Check Youself 10

State the following statements as true or false.

a.If a line d is perpendicular to a plane P then the plane which includes line d is perpendicular to plane P.

b.If three planes are perpendicular to each other their intersection is a point.

c.When three planes are perpendicular to each other the intersection lines of these planes cannot be perpendicular to each other.

d.Two intersecting planes P and Q are perpendicular to the same plane R. So their intersection line is also perpendicular to plane R.

Answers

a)True b) True c) False d) True

D. DISTANCE

Date: 2015-12-11; view: 1305