Distance Between Skew Lines

To find the distance between two skew lines, we find the distance from one of these lines to the plane containing the other and parallel to the first line. This distance is equal to the length of the line segment perpendicular to both lines. Now let us show this.

Let m and n be two skew lines (Figure 1.52). We proved that we can draw a unique plane parallel to m and containing n. Let α be this plane. Through any point P on m, there can be drawn a unique line perpendicular to α and let Q be the intersection of 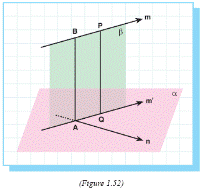this line and α.

Through Q let us draw line m' parallel to m. m' is in α.

Since m // m', they determine a plane β. Let A be the intersection of m' and n.

Through A there can be drawn a unique line

parallel to PQ.

This line will be in plane β. So it intersects line m at a point B.

Since PQ ⊥ α, PQ ⊥ m'. Since m // m' , PQ ⊥ m. So BA ⊥ m.

Since PQ ⊥ α and BA // PQ, BA ⊥ α. So BA ⊥ n. Therefore,

BA is perpendicular to both m and n.

Hence BA is called as common perpendicularof m and n.

Definition (common perpendicular)

The line segment perpendicular to two given skew lines is called as the common perpendicular of the given skew lines.

Theorem:The common perpendicular of two skew lines is unique.

Proof:

Let m and n be two skew lines and AB be

their common perpendicular.

Let C be a point on n (Figure 1.53).

Since ∠ABC = 90°, AC can not be perpendicular to n. So there

can not be drawn any other common perpendicular containing A or B.

Now let us show that there is not any other

common perpendicular except AB.

Assume that CD is a line segment perpendicular to both m and n. Let m' be the line parallel to m and passing through B. Since n and m' are intersecting lines, they determine a plane α.

So AB ⊥ α . Since CD ⊥ m, CD ⊥ m' .

So CD ⊥ α too. Since AB ⊥ α and CD ⊥ α, AB // CD .

Then points A, B, C, D will be coplanar which is impossible.

Hence the common perpendicular is unique

Now, let us show that the length of the common perpendicular is the smallest distance between two skew lines.

Let m, n be two skew lines and α be the plane containing n and parallel to m. Let AB be the common perpendicular of m and n, and m' be the line passing through B and parallel to m. Let P and R be any two other points on m and n. (Figure 1.54)

Through P let us draw a line parallel to AB and let Q be the intersection of α and this line. Since AB ⊥ α and PQ // AB, PQ ⊥ α.

So, we have that PQBA is a rectangle and AB = PQ .

Since PQ ⊥ α, PQ ⊥ QR. Therefore PR > PQ and since PQ = AB, PR > AB.

So we can conclude that any line segment drawn between two skew lines is longer than their common perpendicular.

(To summarize: the length between two skew lines is the length of the common perpendicular of these lines. This length is equal to the distance from one of them to the plane containing the other and parallel to the first line.)

Example 37:From a point P to a plane α, perpendicular PA and two inclined line segments

PB and PC are drawn. Given that,

PB = PC ,

m(∠BPA) = 45°,

m(∠BPC) = 60°, and

PA = 2ñ2 cm, find BC.

Solution:

Since PA ⊥ α, PA ⊥ AB, and since ∠BPA = 45° ,

PB = PA ^.ñ2 = 2ñ2 ^. ñ2 then PB = 4 cm.

Since PB = PC and ∠BPC = 60°,

DPBC is an equilateral triangle.

So BC = PB = 4 cm.

Example 38:A line segment AB intersects a plane α at a point C. If 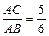and the distance between B and α is 2 cm, find the distance between A and α.

Solution:Let BP ⊥ α and AQ ⊥ α where P, Q are in α.

Then BP // AQ.

They determine a plane β and the intersection of this plane and α is line PQ (Figure 1.57).

Since A and B are in plane β, line AB is in β.

So AB and PQ intersect and this intersection is in α. Since AB intersects α at C, the intersection point is C. So P, C and Q are collinear.

Since PB // AQ, DBPC DAQC.

So we have .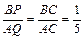

AQ = 5 ^. BP = 5 ^. 2 = 10 cm.

Example 39:From a point A to a plane α, perpendicular AB is drawn. If the distance from B to m is 6 cm and AB = 8 cm, find the distance

from A to m. (m is a line in α)

Solution:Let BP ⊥m (Figure 1.59). Then BP = 6 cm.

Since AB ⊥ α and BP ⊥ m, by the three perpendiculars theorem, AP ⊥ m.

So the distance from A to m is AP.

Since AB ⊥ α, AB ⊥ BP.

So .

Example 40:ABCD is a rhombus and P is a point not in (ABC) so that

PA ⊥ (ABC). Find the distance between lines PC and BD if PA = AB = 4 cm and ∠DAB = 60° .

Solution:Let M be the intersection point of diagonals AC and DB.

Let MN be perpendicular to PC.

Let us show that MN ⊥ DB too.

Since PA ⊥ (ABC) , PA ⊥ AB and PA ⊥ AD.

Since AD = AB and ∠PAB = ∠PAD,

DPAB @ DPAD (S.A.S.)

So PD = PB.

Since PD = PB and DC = BC , DPDC @ DPBC (S.S.S.).

So ∠NCD = ∠NCB.

Then DNCD @ DNCB (S.A.S.).

So ND = NB, DM = MB, and DNDM @ DNBM (S.S.S.).

Thus we get ∠NMD = ∠NMB = 90°.

Hence NM is the common perpendicular of DB and PC.

So the distance between PC and DB is the length of MN.

Now let us find MN.

∠DAB = 60° , AB = 4 cm, and PA = 4 cm are given. Then AM = 2ñ3 cm and

MC = 2ñ3 cm.

Since PA ⊥ (ABC), PA ⊥ AC. Then 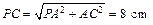, DCMN DCPA

(A.A.A.)

So , , 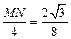cm.

Example 41:Side AB of triangle ABC is in a plane α. Find the distance from

C to α if the distance from the centroid to α is 2 cm.

Solution: Let G be the centroid of DABC,

GQ ⊥ α, and CP ⊥ α (Q and P are in α).

Let M be the midpoint of AB.

C, G, M are collinear.

Since GQ ⊥ α and CP ⊥ α, GQ and CP are

in the same plane.

Since G and C are in this plane, M is also in

this plane.

Since M, Q, P are intersections of this plane and α, they are on the same line.

Then GQ // CP and DMGQ DMCP.

So . GQ = 2 cm is given. So CP = 6 cm.

Example 42:m and n are two lines parallel to a plane α and they are on the same side of α. If the distances from m and n to α are equal, can m and n be skew lines?

Solution:

Let A and B be points on m and n respectively.

Let A₁ and B₁ be two points in α such that

BB₁ ⊥ α and AA₁ ⊥ α.

Given that m and n are equidistant from α.

So AA₁ = BB₁.

Since AA₁ ⊥ α and BB₁ ⊥ α, AA₁ ⊥ B₁A₁ and

BB₁ ⊥ B₁A₁.

Moreover BB₁ // AA₁. So AA₁B₁B is a rectangle. So AB // A₁B₁.

Then AB and m determine a plane parallel to α.

Through B there can be drawn only one plane parallel to α.

So n is in the plane determined by m and AB.

Therefore m and n are coplanar. So they cannot be skew lines.

Example 43:A, B, C are three points in a plane α and M is a point not in α so that MB ⊥ α. If MB = 3 cm, ∠MAB = 60°, and ∠MCB = 45°, what is the maximum length of line segment AC in cm?

Solution:Since MB⊥ α, MB⊥AB and MB⊥BC.

MB = 3 cm, ∠MAB= 60°, ∠MCB = 45 are given.

So AB = ñ3 cm and BC = 3 cm.

AC is maximum if A, B, C are collinear.

Because if they are noncollinear in DABC AC < AB + BC.

So the maximum length is AB + BC = 3 + ñ3 cm.

Example 44:DABC is an equilateral triangle with a side of 1 cm. M is a point not in (ABC). If MB ⊥ (ABC), what is the distance between lines MB and AC in cm?

Solution:Let BH ⊥ AC.

Since MB ⊥ (ABC), MB ⊥ BH.

So BH is the common perpendicular of MB and AC.

DABC is an equilateral triangle.

So BH = cm is the distance between the lines MB and AC.

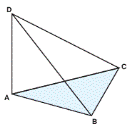
Example 45:ABCD is a square and MA ⊥ (ABC). If MA = 2AB,

what is cos ∠BMC?

Solution:Let AB = a.

Then MA = 2a and AC = añ2.

Since MA ⊥ (ABC), MA ⊥ AB and MA ⊥ AC.

Then and

.

Since MA ⊥ (ABC) and AB ⊥ BC by three perpendiculars theorem MB ⊥ BC.

So, .

Example 46:In the adjacent figure, DA ⊥ (ABC).

If m(∠ABD) = m(∠ADC) = 60° and m(∠BDC) = 45°.

What is cos (∠BAC) ?

Solution:

Since DA ⊥ (ABC), DA ⊥ AB and DA ⊥ AC.

Let AB = a.

Then AD = añ3, DB = 2a, AC = ñ3 ^. AD = 3a, DC = 2AD = 2añ3.

Then in DBDC by cosine thorem:

In DABC by cosine theorem:

Equalizing these two equations gives us: .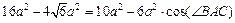

So, and .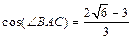

Example 47:In the figure, ABCD is a square, O is the center of ABCD and PO ⊥ (ABC).

Given that, AB = 6 cm and PO = 4 cm.

What is the distance between lines AD and PC?

Solution:Since AD//BC, AD//(PBC).

So we need to find the distance from AD to (PBC).

Since PO ⊥ (ABC) PO ⊥ OB, PO ⊥ PC.

Then and .

Since OB = OC, PB = PC.

Let E be the midpoint of BC.

Since PB = PC, PE ⊥ BC.

Then draw EO. Let EO intersect AD at F.

Since EB = EC and O is the center of ABCD then EF//AB. So BC ⊥ EF.

BC ⊥ EF, BC ⊥ PE. So BC ⊥ (PFE).

Let FH ⊥ PE. Since BC ⊥ (PFE) then BC ⊥ FH.

FH ⊥ BC, FH ⊥ PE. So FH ⊥(PCB).

Therefore the distance from AD to (ABC) is FH. Now let us find FH.

cm.

cm.

Check Yourself 11

1.A and B are two points equidistant from a plane α and they are on the same side of α. Show that AB // α.

2.In the adjacent figure, PQ is a line segment on one

side of α. If the distances from P and Q to α are 4

cm and 6 cm respectively, find the distance from the

midpoint of PQ to α.

3.DABC is a triangle on one side of a plane α.

If the distances from vertices A, B, and C to α are 6 cm,

8 cm, and 10 cm respectively, find the distance

from the centroid of DABC to plane α.

4.ABCD is a rhombus and PA ⊥(ABC). If ∠BAD = 60° and AC = 2ñ3, find the distance between lines PA and BC.

5.m and n are two lines parallel to a plane α and they are on the same side of α. If the distances from m and n to α are equal, can m and n be skew lines?

Answers

2.5 3.8 4.

5.No. They are intersecting, coincident or parallel lines.

EXERCISES 2

Date: 2015-12-11; view: 3598