I. The point is on the line.

Let d be a line and A be a point on d.

Let us take two distinct planes α and β containing d.

(Figure 1.38)

Let m be the line lying in α and perpendicular to d at A and n be the line lying in β and perpendicular to d at A.

Then m and n determine a unique plane λ perpendicular to d.

ii. The point is not on the line.

Let d be a line and A be a point in space not on d.

Line d and point A determine a plane α (Figure 1.39).

In α there can be drawn a line m passing through A and perpendicular to d at a point B.

Let β be another plane containing line d.

In β, through point B, let us draw a line n perpendicular to d.

Since m and n are intersecting lines, they determine a plane λ.

Since d is perpendicular to two intersecting lines in λ (those are m and n), d is perpendicular to λ.

Now let us prove that this plane is unique.

Let d be a line and A be a point not on d.

Assume that through A there can be drawn more than one plane perpendicular to d (Figure1.40).

Let α and β be two of these planes.

Let B be the intersection of d and α, and C be the intersection of d and β.

Then d ⊥ AB and d ⊥ AC which is impossible because DABC cannot have two right angles.

3.Let m and d be two parallel lines and α be a plane such that m ⊥ α. We need to show that d ⊥ α. (Figure 1.41)

Since m ⊥ α, m is perpendicular to every line in α.

It is proven that if one of two parallel lines is

perpendicular to a third line then the other one is perpendicular to the same line.

So d is perpendicular to every line in α too.

Therefore d ⊥ α.

4.Let lines d and b be perpendicular to a plane α (Figure 1.42).

On b, take a point B which is not in α and through B, draw a line b₁ parallel to d.

If b and b₁ are not coincident they determine a

plane β.

Let m be the intersection of β and α.

Since b₁ // d and d ⊥ α, b₁ ⊥ α. So b₁ ⊥ m.

Since b is perpendicular to α, b is also perpendicular to m.

However through B there can be drawn only one line perpendicular to α.

Hence b₁ and b are coincident.

That means lines d and b are parallel.

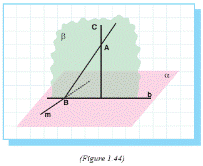
5.Let α be a plane and A be a point.

In α take a line m (if A is in α take m in such a way that A is not on m) (Figure 1.44).

Through A there can be drawn a plane β perpendicular to m.

α and β are intersecting planes because m intersects β at a point B and m is in α.

So α and β have a common line b.

In β through A there can be drawn line c perpendicular to b.

Then since c ⊥ b and c ⊥ m, it can be concluded that c ⊥ α.

Now let us prove that this line is unique.

Let α be a plane and A be a point not in α.

Assume that through A there can be drawn more than one line perpendicular to α.

Let c and c' be two of these lines.

Since c and c' perpendicular to α, they intersect α.

Let B and C be the intersection points. B and C determine a line n. (Figure 1.45)

Since c ⊥ α, c ⊥ n and since c' ⊥ α, c' ⊥ n. Then DABC is a triangle with two right angles which is impossible.

So through A we can draw only one line perpendicular to α.

6. Let α and β be two parallel planes and m be a line perpendicular to α. (Figure 1.46)

Since m is perpendicular to α, it intersects α at a point A.

If a line intersects one of two parallel

planes, it intersects the other too. So m intersects β at a point B.

In α, let us take two lines d and b intersecting at A.

Let d' be the intersection of β and the plane determined by d and m, and let

b' be the intersection of β and the plane determined by m and b.

When two parallel planes are intersected by a plane the intersections are parallel. d' // d and b' // b.

Since m ⊥ α, m ⊥ d and m ⊥ b. So m ⊥ d' and m ⊥ b'.

Since m is perpendicular to two intersecting lines in β, m is perpendicular to β.

Theorem: (Three Perpendiculars Theorem)

A line drawn in a plane through the foot of an inclined line is perpendicular to the projection of the inclined line if and only if it is perpendicular to the inclined line itself.

Proof:

In this theorem we need to prove that

1.If a line drawn in a plane through the foot of an inclined line is perpendicular to the projection of the inclined line, it is perpendicular to the inclined line.

2.If a line drawn in a plane through the foot of an inclined line is perpendicular to the inclined line, it is perpendicular to the projection of the inclined line.

1.Let m be the line lying in a plane α perpendicular to the projection of an inclined line d onto α at point B which is the intersection

of d and α.

Let A be any point on d and let the perpendicular

drawn through A intersect α at C (Figure 1.43).

Point C is on the projection of d.

CB and d determine a plane β. Since AC ⊥ α,

AC ⊥ m.

Given that m ⊥ CB, so m ⊥ β and m ⊥ d.

2.Referring to the same figure, we need to prove that if m ⊥ d then m ⊥ CB. Since m is perpendicular to two intersecting lines in β which are d and AC, it is perpendicular to β.

So it is perpendicular to CB.

Example 27:DABC is an isosceles right triangle such that AB = BC = 4 cm. P is a point not in plane (ABC) and M is the midpoint of AC. If PB ⊥ AB, PB ⊥ BC and PB = cm, find PM.

Solution:

AC is the hypotenuse of DABC, AC = cm.

Since BM is the median of the hypotenuse, BM = cm.

Since PB ⊥ BC and PB ⊥ AB , PB ⊥ (ABC).

So PB ⊥ BM.

Then PM² = PB² + BM² = 8 + 8 = 16, PM = 4 cm.

Example 28:Show that if two planes α and β are perpendicular to a line m

then they are parallel.

Solution:

Since m is perpendicular to α and β, it intersects both planes.

Let A and B be the intersections.

Assume that α and β are not parallel. Then they will have a common point P.

Since AP is in α, m ⊥ AP and since BP is in β, m ⊥ BP.

So DAPM is a triangle with two right angles which is impossible.

Therefore α and β can not have any common point which means α // β.

Example 29: In the adjacent figure, DABC is in the plane α, PC ⊥ α, and AC ⊥ CB.

If ∠CAB = 30° and ∠PBC = 45°, find the

cosine of angle ∠APC.

Solution:

Since PC ⊥ α, PC ⊥ CA and PC ⊥ CB.

If AB = a then CB = and CA = .

Since ∠PBC = 45°, CP = CB = .

So ∠APC = 60° and cos ∠APC = .

Example 30:Line m is inclined to a plane α. Show that through m, there can

be drawn one and only one plane perpendicular to α.

Solution:

Let m intersect α at A, and B be another point

on m.

There can be drawn a line d passing through B and perpendicular to α.

Then since d and m are intersecting lines they determine a plane β.

In β there is a line (line d) perpendicular to α.

Therefore, β ^ α.

Now, let us prove that this plane is unique.

Assume that there are planes β₁ and β₂ containing m and perpendicular to α.

Then through a point on m there can be

drawn line segments AB and BC perpendicular to

α (A and C are in α).

Then BA ⊥ AC and BC ⊥ AC which is impossible.

Therefore, there can not be drawn more than one plane perpendicular to α through m.

Example 31:In figure, PC ⊥ (ABC) ,

∠ACB = 90° ,

PM ⊥ AB, and

AM = MB.

Find m(∠CAB).

Solution:

And .

Then, since AM = MB, PA = PB.

Since PC ⊥ (ABC), PC ⊥ AC and PC ⊥ CB .

Then, and .

Since PA = PB, CA = CB.

So DABC is an isosceles right triangle and m(∠CAB) = 45° .

Example 32:In the adjacent figure, PB ⊥ (ABC), DABC is an equilateral triangle, and M and N are midpoints of AB and BC respectively.

What is the ratio of the area of DPCA to the area of DPNM if PB = AB ?

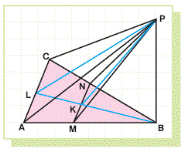Solution:

It is given that PB ⊥ (ABC).

So PB ⊥ BC and PB ⊥ BA.

Since AB = BC, PA = PC, and since BN = BM,

PM = PN.

Let L and K be the midpoints of AC and MN respectively.

Since DPCA and DPMN are isosceles triangles, PL ⊥ AC and PK ⊥ MN.

Hence .

Let us take CA = a.

Then AB = BC = PB = a, MN =

, Since PB ⊥ (ABC), PB ⊥ BL.

So 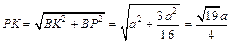and

.

Then .

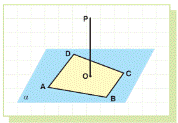
Example 33:In the given figure, ABCD is a quadrilateral in a plane α.

P is a point not in α such that PO ^ α.

If PA = PB = PC = PD, find ∠DAB + ∠BCD.

Solution:

Since PO ⊥ α, PO is perpendicular to all OA, OB, OC and OD.

Then since PA = PB = PC = PD and

∠POA = ∠POB = ∠POC = ∠POD = 90° ,

OA = OB = OC = OD.

So, O is the center of the circumscribed

circle of ABCD i.e, ABCD is a cyclic quadrilateral.

Therefore ∠DAB + ∠BCD = 180°.

Example 34:In figure, A, B, C are on d, A₁, B₁, C₁ are in α such that AA₁ ⊥ α, BB₁ ⊥ α and CC₁ ⊥ α .

Show that A₁, B₁, C₁ are collinear.

Solution:Since AA₁, BB₁ and CC₁ are perpendicular to α, they are parallel

lines.

Since AA₁ // BB₁, they determine a plane β.

Since A and B are in β, d is in β. So C is in β.

Since BB₁ // CC₁, CC₁ is in the plane containing BB1 and C.

So CC₁ is also in β.

Since A₁, B₁, C₁ are intersections of α and β, they are collinear.

Check Yourself 9

1.In the adjacent figure, PA ⊥ α ,

∠BPA = 20°,

∠CPA = 10°, and

∠APD = 30° .

Write PB, PC, PD in ascending order.

2.In the adjacent figure, M is the midpoint of CB and

PM ⊥ (ABC).

If MC = CA and PA = PB = PC,

find ∠ABC.

3.Lines a, b, c are coplanar and line d is not in the plane containing a, b, c. It is given that d is perpendicular to a and b but it is not perpendicular to c.

What can be concluded about a and b?

4.DABC is right angled at A, lies in a plane α and PA ⊥ α where P is a point not in α. If A is equidistant from points B, C and P, find ∠BPC .

5.State the followings as true or false

a)If two lines are perpendicular to the same line, they are parallel.

b)If two lines are perpendicular to the same plane, they are parallel.

c)If a line is perpendicular to two lines lying in a plane, it is perpendicular to the plane.

Answers

1.PC < PB < PD 2.30° 3.a // b4.60°

5.a) False b) True c) False

Date: 2015-12-11; view: 1842