
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Example
The example shows the construction of the Shannon code for a small alphabet. The five symbols which can be coded have the following frequency:
| Symbol | A | B | C | D | E |
| Count | |||||
| Probabilities | 0.38461538 | 0.17948718 | 0.15384615 | 0.15384615 | 0.12820513 |
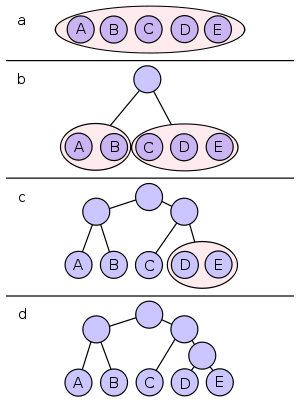
All symbols are sorted by frequency, from left to right (shown in Figure a). Putting the dividing line between symbols B and C results in a total of 22 in the left group and a total of 17 in the right group. This minimizes the difference in totals between the two groups.
With this division, A and B will each have a code that starts with a 0 bit, and the C, D, and E codes will all start with a 1, as shown in Figure b. Subsequently, the left half of the tree gets a new division between A and B, which puts A on a leaf with code 00 and B on a leaf with code 01.
After four division procedures, a tree of codes results. In the final tree, the three symbols with the highest frequencies have all been assigned 2-bit codes, and two symbols with lower counts have 3-bit codes as shown table below:
| Symbol | A | B | C | D | E |
| Code |
Results in 2 bits for A, B and C and per 3 bits for D and E an average bit number of

Shannon–Fano Algorithm
Date: 2014-12-28; view: 1506
| <== previous page | | | next page ==> |
| Code of Shannon - Fano and its properties. | | | Nasal Foreign Bodies |