Code of Shannon - Fano and its properties.

In the field of data compression, Shannon–Fano coding, named after Claude Shannon and Robert Fano, is a technique for constructing a prefix code based on a set of symbols and their probabilities (estimated or measured). It is suboptimal in the sense that it does not achieve the lowest possible expected code word length like Huffman coding; however unlike Huffman coding, it does guarantee that all code word lengths are within one bit of their theoretical ideal 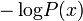. The technique was proposed in Shannon's "A Mathematical Theory of Communication", his 1948 article introducing the field of information theory. The method was attributed to Fano, who later published it as a technical report. Shannon–Fano coding should not be confused with Shannon coding, the coding method used to prove Shannon's noiseless coding theorem, or with Shannon–Fano–Elias coding (also known as Elias coding), the precursor to arithmetic coding.

In Shannon–Fano coding, the symbols are arranged in order from most probable to least probable, and then divided into two sets whose total probabilities are as close as possible to being equal. All symbols then have the first digits of their codes assigned; symbols in the first set receive "0" and symbols in the second set receive "1". As long as any sets with more than one member remain, the same process is repeated on those sets, to determine successive digits of their codes. When a set has been reduced to one symbol, of course, this means the symbol's code is complete and will not form the prefix of any other symbol's code.

The algorithm produces fairly efficient variable-length encodings; when the two smaller sets produced by a partitioning are in fact of equal probability, the one bit of information used to distinguish them is used most efficiently. Unfortunately, Shannon–Fano does not always produce optimal prefix codes; the set of probabilities {0.35, 0.17, 0.17, 0.16, 0.15} is an example of one that will be assigned non-optimal codes by Shannon–Fano coding.

For this reason, Shannon–Fano is almost never used. Shannon–Fano coding is used in the IMPLODE compression method, which is part of the ZIP file format.

A Shannon–Fano tree is built according to a specification designed to define an effective code table. The actual algorithm is simple:

1. For a given list of symbols, develop a corresponding list of probabilities or frequency counts so that each symbol’s relative frequency of occurrence is known.

2. Sort the lists of symbols according to frequency, with the most frequently occurring symbols at the left and the least common at the right.

3. Divide the list into two parts, with the total frequency counts of the left part being as close to the total of the right as possible.

4. The left part of the list is assigned the binary digit 0, and the right part is assigned the digit 1. This means that the codes for the symbols in the first part will all start with 0, and the codes in the second part will all start with 1.

5. Recursively apply the steps 3 and 4 to each of the two halves, subdividing groups and adding bits to the codes until each symbol has become a corresponding code leaf on the tree.

Date: 2014-12-28; view: 1656