
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Orthogonal decomposition of signals with limited spectrum range.
What are the functions of autonomic nervous system?
How is acetylcholine synthesized and terminated at the nerve terminals? At what sites acetylcholine is released?
Describe the synthesis, storage, release and termination of norepinephrine at the postganglionic sympathetic nerve terminals.
What do you understand by uptake (reuptake) of norepinephrine? What is its significance?
What are the different types of cholinoceptors and their location?
What are muscarinic and nicotinic actions of acetylcholine?
Classify cholinomimetic drugs.
Compare choline esters regarding receptor specificity and hydrolysis by acetylcholinesterases.
Which alkaloids have cholinergic effects? What are the uses and adverse effects of carbachol and pilocarpine?
Describe the effects of cholinergic drugs on different organ systems.
List the drugs which inhibit cholinesterases. What are their uses and adverse effects? How are these adverse effects treated?
Write prescriptions for next drugs and note their indications and contraindications (precautions):
1. Direct-acting cholinomimetic that is lipid-soluble and is favored in the treatment of glaucoma
2. Indirect-acting cholinomimetic with a duration of many days; used in the treatment of glaucoma
3. Indirect-acting carbamate cholinomimetic; poor lipid solubility; duration of action about 2-4 hours
4. An ester of carbaminic acid, resistant to cholinesterase, orally active, poor lipid solubility, acting mainly on muscarinic cholinoceptors.
5. Agent that is normally released from sympathetic nerve endings innervating thermoregulatory sweat glands
6. Indirect-acting cholinomimetic, tertiary amine, lipid soluble; duration of action 30 minutes to 2 hours.
7. Indirect-acting carbamate cholinomimetic, quarternary amine, poor lipid solubility, orally active, duration of action 4 to 8 hours.
8. Indirect-acting cholinomimetic, alcohol, quarternary amine, poor lipid solubility, not orally active; 5-15 minutes duration of action
9. An ester of carbaminic acid, resistant to cholinesterase, orally active, poor lipid solubility, acting on both types of cholinoceptors.
10. Indirectly acting drug that releases norepinephrine and dopamine from their nerve endings
| Amphetamine | T.5,10-PO |
| Acethylcholine | 10/ml-Eye drops |
| Betanechol | T.5,10,25,50-PO; A.5/ml-SC |
| Carbachol | 0.75, 1.5, 2.25, 3% Eye drops - Top |
| Pilocarpine | 0.25,0.5,1,2,3,4,6,8, 10%-Eye drops, 4%-Eye gelum |
| Echothiophate | 0.03%, 0.06, 0.125, 0.25%-Eye drops |
| Edrophonium | 10/ml-IV, IM injections |
| Neostigmine | T.15-PO, 0.1%-10 ml,0.05%,0.025%-1 ml solutions for injections |
| Pyridostigmine | T.60,180, 5/ml-IV, IM-for injections |
| Physostigmine | 0.25, 0.5%-Eye drps; 0.25%-Eye ointment, 1/ml-IV,IM |
5. Teaching methods – working in pairs, the prescription writing of drugs for concrete situations; training, defining terms, solving problems, answer questions, working out examples (of the slides, of the handbooks and handouts), MCQs.
6.Literature
1.Katzung B. G., ed. 2001. Basic and Clinical Pharmacology, 8th ed., Lange Medical Books/McGraw-Hill, Appleton and Lange. PP. 107-119, 446-462.
2.Katzung B.G., Trevor A.J., ed. 1998, Examination & Board Rewiew. 5th ed., Stamford, Connecticut, Appleton & Lange. PP. 61-68, 205-212.
2.Tripathi K.D., ed.1999, Essentials of Medical Pharmacology. 4th ed., New Delhi, India, Jaypee Brothers. PP. 103-114, 148-159.
3.Sharma V.N., ed.1996 Essentials of Pharmacology. 1th ed., New Delhi, India, CBS Publishers & Distributors. PP. 54-58, 69-70, 119-125.
7. Assessment Prescriptions Writing, MCQs, ECQs.
Orthogonal decomposition of signals with limited spectrum range.
As well as the Fourier transform for periodic and non-periodical FIR signals, widely used Kotelnikov decomposition. Let us consider the main features of these expansions.
Orthogonal decomposition of Kotelnikov for continuous signals with bounded spectra can represent them and a pulse sequences. The theoretical basis of the presentation is Kotelnikov theorem (sampling theorem): any continuous function S(t), does not contain frequencies above F, completely determined by the sequence of values in moment you are separated from each other for a while 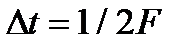 . The total number of samples to signal duration
. The total number of samples to signal duration 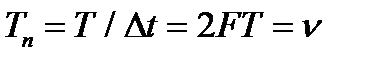 , ie, the same base signal.
, ie, the same base signal.
For the signal S (t), the spectrum of which is in the interval [0, F] [15], orthogonal decomposition Kotelnikov
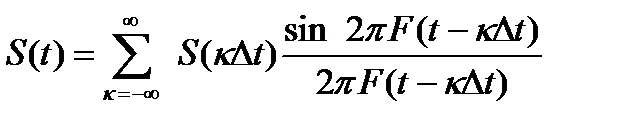
Where 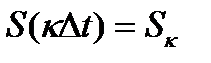 - countdown signal at the moment
- countdown signal at the moment 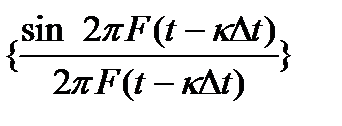 basis set of orthogonal functions with a common
basis set of orthogonal functions with a common 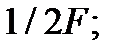
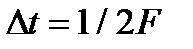 — sampling interval equal to the norm of basic function. Functions
— sampling interval equal to the norm of basic function. Functions 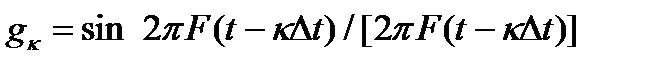 is call reference functions and values
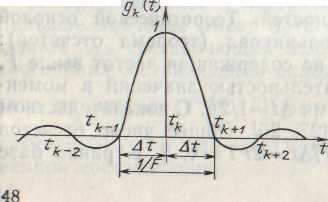
is call reference functions and values 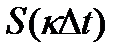 - counts. Graph of samples shown in figure Orthogonality of samples tested by calculating the integral
- counts. Graph of samples shown in figure Orthogonality of samples tested by calculating the integral
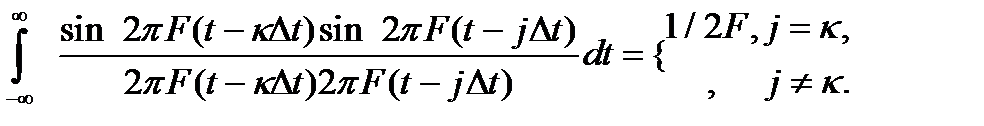
The sampling interval, as we see, does not exceed half of the highest frequency of the signal.
From Parseval that the energy of a continuous signal with a limited range determined by counting:
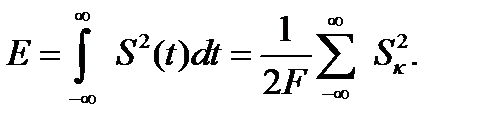
Once again it must be emphasized that in nature there are no signals, co-torye have both limited duration and spectrum. In engineering calculations must take into account that part of the spectrum, which are home to 80 ... 95% of the signal energy. So particle of most of the signals are considered as signals with limited spectrum. If there is a signal on the interval 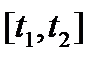 , then choose the number of terms (number of samples)
, then choose the number of terms (number of samples) 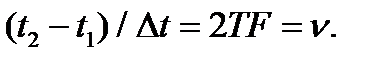
Advantages of an orthogonal decomposition Kotelnikov following: a basic system of orthogonal functions is chosen so that the series is formal, that is, at any point of reference he makes one value the other components of a number of degenerate to zero: coefficients of the series can not compute, and their values are determined by measuring the signal.
Graph of samples:
Or from its analytical form, and knowing the signal duration T and
cut-off frequency F, determine the required number of samples of the signal energy 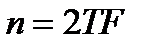 .
.
At the last features useful in more detail. For this, consider the physical meaning of the Kotelnikov decomposition. Each term of the sum is response of an ideal low-pass filter gk (see Fig.) with a cutoff frequency of F for a very short pulse arriving at the time 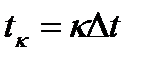 and space
and space 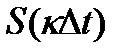 available. Therefore, when a discrete signal transmission S (t) with a limited range to at regular intervals to take instant readings i peny signal and transmit the channel sequence sufficiently short pulses of amplitude at the time
available. Therefore, when a discrete signal transmission S (t) with a limited range to at regular intervals to take instant readings i peny signal and transmit the channel sequence sufficiently short pulses of amplitude at the time 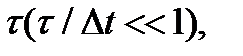 selected to the receiver in the selected sequence video pulses passed through a low pass filter, the output of which transmits a continuous signal is restored. Pulse duration τ can be arbitrarily small, but choose it based on the transparency of the link bandwidth. hour- u rate (clock speed) is 2F.
selected to the receiver in the selected sequence video pulses passed through a low pass filter, the output of which transmits a continuous signal is restored. Pulse duration τ can be arbitrarily small, but choose it based on the transparency of the link bandwidth. hour- u rate (clock speed) is 2F.
Date: 2014-12-28; view: 1519
| <== previous page | | | next page ==> |
| The main questions of the theme | | | Code of Shannon - Fano and its properties. |