Elliptic functions

The theory of functions of a complex variable was also being decisively reformulated. At the start of the 19th century, complex numbers were discussed from a quasi-philosophical standpoint by several French writers, notably Jean Robert Argand. A consensus emerged that complex numbers should be thought of as pairs of real numbers, with suitable rules for their addition and multiplication so that the pair (0, 1) was a square root of -1. The underlying meaning of such a number pair was given by its geometric interpretation either as a point in a plane or as a directed segment joining the coordinate origin to the point in question. (This representation is sometimes called the Argand diagram.) In 1827, while revising an earlier manuscript for publication, Cauchy showed how the problem of integrating functions of two variables can be illuminated by a theory of functions of a single complex variable, which he was then developing. But the decisive influence on the growth of the subject came from the theory of elliptic functions.

The study of elliptic functions originated in the 18th century, when many authors studied integrals of the form

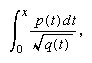
where p(t) and q(t) are polynomials in t and q(t) is of degree 3 or 4 in t. Such integrals arise naturally, for example, as an expression for the length of an arc of an ellipse (whence the name). These integrals cannot be evaluated explicitly; they do not define a function that can be obtained from the rational and trigonometric functions, a difficulty that added to their interest. Elliptic integrals were intensively studied for many years by the French mathematician Legendre, who was able to calculate tables of values for such expressions as functions of their upper endpoint, x. But the topic was completely transformed in the late 1820s by the independent but closely overlapping discoveries of two young mathematicians, the Norwegian Niels Henrik Abel and the German Carl Gustav Jacob Jacobi. These men showed that, if one allowed the variable x to be complex and the problem were inverted, so that the object of study became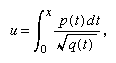

considered as defining a function x of a variable u, then a remarkable new theory could be discovered. The new function, for example, possessed a property that generalized the basic property of periodicity of the trigonometric functions sine and cosine: sin (x) = sin (x + 2π). Any function of the kind just described has two distinct periods, ω₁ and ω₂:

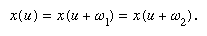
These new functions, the elliptic functions, aroused a considerable degree of interest from the first because many interesting and novel things could be said about them. The analogy with trigonometric functions ran very deep (indeed the trigonometric functions turned out to be special cases of elliptic functions), but their greatest influence was on the burgeoning general study of functions of a complex variable. The theory of elliptic functions became the paradigm of what could be discovered by allowing variables to be complex instead of real. But their natural generalization to functions defined by more complicated integrands, although it yielded partial results, resisted analysis until the second half of the 19th century.

Date: 2015-01-29; view: 942