
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Encyclopædia Britannica, Inc.
Thus, in Figure 4 the familiar graph of a parabola y = x2 is continuous around the point x = 0; as x varies by small amounts, so necessarily does y. On the other hand, the graph of the function that takes the value 0 when x is negative or zero, and the value 1 when x is positive, plainly has a discontinuous graph at the point x = 0, and it is indeed discontinuous there according to the definition. If x varies from 0 by any small positive amount, the value of the function jumps by the fixed amount 1, which is not an arbitrarily small amount.
Cauchy said that a function f(x) tends to a limiting value 1 as x tends to the value a whenever the value of the difference f(x) - f(a) becomes arbitrarily small as the difference x − a itself becomes arbitrarily small. He then showed that, if f(x) is continuous at a, the limiting value of the function as x tended to a was indeed f(a). The crucial feature of this definition is that it defines what it means for a variable quantity to tend to something entirely without reference to ideas of motion
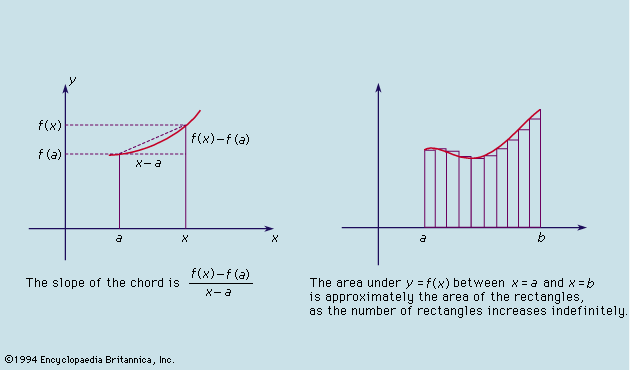
Figure 5: Differentiation and integration.
Encyclopædia Britannica, Inc.
Cauchy then said a function f(x) is differentiable at the point a if, as x tends to a (which it is never allowed to reach), the value of the quotient {f(x) - f(a)}/(x - a) (see Figure 5, left) tends to a limiting value, called the derivative of the function f(x) at a. To define the integral of a function f(x) between the values a and b, Cauchy went back to the primitive idea of integral as the measure of the area under the graph of the function. He approximated this area by rectangles and said that, if the sum of the areas of the rectangles tends to a limit as their number increases indefinitely (see Figure 5, right) and if this limiting value is the same however the rectangles are obtained, then the function is integrable. Its integral is the common limiting value. After he had defined the integral independently of the differential calculus, Cauchy had to prove that the processes of integrating and differentiating are mutually inverse. This he did, giving for the first time a rigorous foundation to all the elementary calculus of his day.
II. Suggest the right translation of the Infinitive in the sentences:
1.…his methods gradually became established and refined to form the core of the modern rigorous calculus, a subject now called mathematical analysis.
2.…the much-needed degree of precision they bring to mathematics has proved difficult to appreciate.
III. What does the word "either" stand for? Study the context to understand it and translate the sentence into Russian.
Cauchy provided a novel underpinning by stressing the importance of the concept of continuity, which is more basic than either.
IV. How do you understand the word " diet " in the sentence? Suggest your own interpretation and translate the sentence into Russian.
Lagrange, who favoured a more traditional and theoretical diet of advanced calculus and rational mechanics…
V. Read the first three paragraphs of the article and pick out the information about Cauchy's contribution to calculus.
VI. Translate the rest of the article at sight.
VII. Match the words with their synonyms:
precision prefer
favour rigour
amount complex
propose refuse
concept suggest
concerned quantity
reject idea
sophisticated independent
autonomous interested
VIII. Fill in the missing forms:
| Noun | Verb | Adjective | Adverb |
| differentiable | |||
| integrate | |||
| continuity | |||
| invent | |||
| independently | |||
| geometry |
IX. Add all the possible words of the word family to the scheme. Support them with translation into Russian and examples.
applicant
apply
X. Suggest the Russian counterparts for the following words and word combinations:
a broad range of phenomena, by virtue of, the foundations of the calculus, to give a satisfactory explanation, a power series expansion, to run the risk of, a vicious circle, the core of the modern rigorous calculus, mathematical analysis, processes of differentiation and integration, the reciprocal relation, to provide a novel underpinning, a continuous function, a differentiable function, an integrable function, roughly speaking, a graph of a parabola, on the other hand, according to the definition, a limiting value, a crucial feature, a variable quantity, a derivative of function, differential calculus, mutually inverse.
Date: 2015-01-29; view: 1243
| <== previous page | | | next page ==> |
| Making the calculus rigorous | | | Elliptic functions |