Work and Rotational Kinetic Energy

As we discussed in Chapter 7, when a force 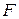causes a rigid body of mass 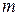to accelerate along a coordinate axis, it does work 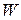on the body. Thus, the body's kinetic energy ( ) can change. Suppose it is the only energy of the body that changes. Then we relate the change 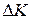in kinetic energy to the work 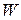with the work-kinetic energy theorem (Eq. 7-10), writing

(work-kinetic energy theorem). (11-41)

For motion confined to an axis, we can calculate the work with Eq. 7-32,

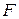This reduces to when is constant and the body's displacement is d.

The rate at which the work is done is the power, which we can find with Eqs. 7-43

(power, one-dimensional motion). (11-43)

Now let us consider a rotational situation that is similar. When a torque accelerates a rigid body in rotation about a fixed axis, it does work 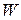on the body. Therefore, the body's rotational kinetic energy ( 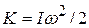) can change. Suppose that it is the only energy of the body that changes. Then we can still relate the change 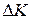in kinetic energy to the work 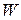with the work-kinetic energy theorem, except now the kinetic energy is a rotational kinetic energy:

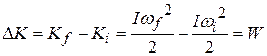(work-kinetic energy theorem). (11-44)

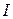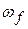Here, is the rotational inertia of the body about the fixed axis and and are the angular speeds of the body before and after the work is done, respectively. Also, we can calculate the work with a rotational equivalent of Eq. 11-42,

(work, rotation about fixed axis),(11-45)

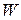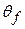where is the torque doing the work , and and are the body's angular positions before and after the work is done, respectively. When is constant, Eq. 11-45 reduces to

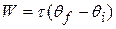(work, constant torque). (11-46)

The rate at which the work is done is the power, which we can find with the rotational equivalent of Eq. 11-43,

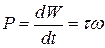power, rotation about fixed axis). (11-47)

Proof of Eqs. 11-44 through 11-47

Let us again consider the situation of Fig. 11-16, in which force rotates a rigid body consisting of a single particle of mass 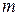fastened to the end of a massless rod. During the rotation, force does work on the body. Let us assume that the only energy of the body that is changed by is the kinetic energy. Then we can apply the work-kinetic energy theorem of Eq. 11-41

. 11-48

Using and Eq 11-18 ( 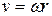) we can rewrite Eq. 11-48 as

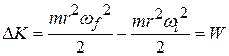
(11-

From Eq. 11-26, the rotational inertia for this one-particle body is 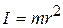. Substituting this into Eq. 11-49 yields

,

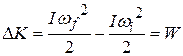which is Eq. 11-44. We derived it for a rigid body with one particle, but it holds for any rigid body rotated about a fixed axis.

We next relate the work 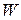done on the body in Fig. 11-16 to the torque оп the body due to force . When the particle moves a distance along its circular path, only the tangential component F_t of the force accelerates the particle along the path. Therefore, only does work on the particle. We write that work 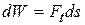. However, we can replace with , where is the angle through which the particle moves. Thus we have

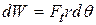. (11-50)

From Eq. 11-32, we see that the product 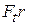is equal to the torque , so we can rewrite Eq. 11-50 as

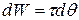(11-51)

The work done during a finite angular displacement from to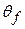

which is Eq. 11-45. It holds for any rigid body rotating about a fixed axis. Equation 11-46 comes directly from Eq. 11-45.

We can find the power P for rotational motion from Eq. 11-51:

which is Eq. 11-47

Sample Problem 11-10

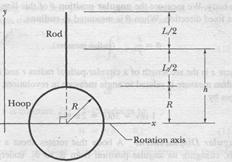
A rigid sculpture consists of a thin hoop (of mass 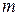and radius = 0.15 m) and a thin radial rod (of mass 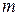and length 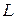= 2.0/ ), arranged as shown in Fig. 11-19. The sculpture can pivot around a horizontal axis in the plane of the hoop, passing through its center.

(a) In terms of 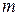and , what is the sculpture's rotational inertia 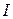about the rotation axis?

A Key Idea here is that we can separately find the rotational inertias of the hoop and the rod and then add the results to get the sculpture's total rotational inertia 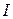. The hoop has rotational inertia 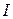_hoop = mR²/2 about its diameter. The rod has rotational inertia 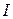_com = mL²/12 about an axis through its center of mass and parallel to the sculpture's rotation axis. To find its rotational inertia 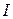_rod about that rotation axis, we use Eq. 11-29, the parallel-axis theorem:

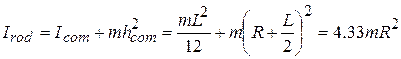
where we have used the fact that 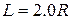and where the perpendicular distance between the rod's center of mass and the rotation axis is . Thus, the rotational inertia / 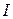of the sculpture about the rotation axis is

(b) Starting from rest, the sculpture rotates around the rotation axis from the initial upright orientation of Fig. 11-19. What is its angular speed 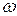about the axis when it is inverted?

SOLUTION: Three Key Ideas are required here:

1.We can relate the sculpture's speed 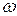to its rotational kinetic energy 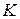with Eq. 11-27 ( ).

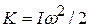2.We can relate 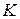to the gravitational potential energy of the sculpture via the conservation of the sculpture's mechanical energy 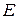during the rotation. Thus, during the rotation, 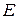does not change ( 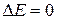) as energy is transferred from to .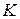

3.For the gravitational potential energy we can treat the rigid sculpture as a particle located at the center of mass, with the total mass concentrated there.

We can write the conservation of mechanical energy ( 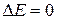) as

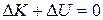
As the sculpture rotates from its initial position at rest to its inverted position, when the angular speed is 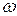, the change 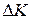in its kinetic energy is

From Eq. 8-7 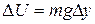, the corresponding change in the gravitational potential energy is

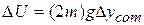
where is the sculpture's total mass, and 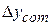is the vertical displacement of its center of mass during the rotation.

To find 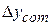, we first find the initial location 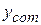of the center of mass in Fig. 11-19. The hoop (with mass 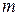) is centered at 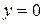. The rod (with mass 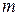) is centered at 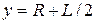. Thus, from Eq. 9-5, the sculpture's center of mass is at

When the sculpture is inverted, the center of mass is this same distance from the rotation axis but below it. Therefore, the vertical displacement of the center of mass from the initial position to the inverted position is

Now let's pull these results together. Substituting Eqs. 11-55 and 11-56 into 11-54 gives us

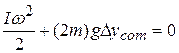
Substituting 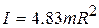from (a) and from above and solving for со, we find

(Answer)

Q. 2.01. Do the internal forces affect the motion of a system under the effect of some external force ?

Ans. No. Torques acting on the system due to internal forces cancel out.

Q. 2.02. What do you mean by a rigid body?

Ans. A body, whose constituent particles remain at their respective positions, when a body is in translational or rotational motion is called a rigid body.

Q. 2.01. Torque and work are both defined as force times distance. Explain, how do they differ.

Ans. (i) Whereas work is a scalar quantity, torque is a vector quantity.

(ii) Work done is measured as the product of the applied force and the distance, which the body covers along the direction of the force. On the other hand, torque is measured as the product of the force and its perpendicular distance from the axis of rotation.

Q.2.02. Why is a ladder more apt to slip, when you are high up on it than when you just begin to climb?

Ans. When a person is high up on a ladder, then torque produced due to his weight about the point of contact between the ladder and the floor becomes quite large. On the other hand, when he starts climbing up, the torque is small. Due to this reason, the ladder is more apt to slip, when one is high up on it.

Q. 2.03. A planet moves around the sun under the effect of gravitational force exerted by the sun. Why is the torque on the planet due to the gravitational force zero?

Ans. The torque on the planet due to the sun,

,

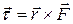where 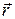is the position vector of the planet w.r.t. the sun and is the gravitational force on the planet. Since the gravitational force on the planet acts along the line joining the planet to the sun, the vectors 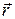and are always parallel and hence .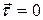

Ans. An object will not acquire angular momentum, if no external torque acts on it. During its flight, a torque acts on the projectile due to gravity and hence it acquires angular momentum.

Q. 2.06. A planet revolves around a massive star in a
highly elliptical orbit. Is its angular momentum constant

1. Starting from Newton's second law of motion, derive the equation of motion of a particle (capable of rotation about an axis) on which a torque 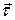is acting. Assume that the motion of the particle is in a plane.

2 Derive expression for torque on a system in cartesian coordinates.

3, Derive expression for the torque acting on a system of 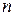-particles.

5. Derive expression for the angular momentum of a system in cartesian co-ordinates.

6. Prove that the time rate of change of the angular momentum of a particle is equal to the torque acting on it.

7. Derive a relation between angular momentum and torque.

8. Derive the relation between the torque and the angular momentum. Hence obtain and state the law of conservation of angular momentum.

9. State and prove the principle of conservation of angular momentum.

B. On Torque

9. A disc of radius 0.5 m is rotating about an axis passing through its centre and perpendicular to its plane.A tangential force of 2,000 N is applied to bring the disk to rest in 2 s. Calculate its angular momentum.

[Ans. 2,000 kg m²/s

10. A torque of 20 N m is applied on a wheel initially at rest. Calculate the angular momentum of the wheel after 3 s.

[Ans. 60 kg m²/s

Type C. On Angular momentum

11. In hydrogen atom, electron revolves in a circular orbit of radius 0.53 A with a velocity of 2.2 x 10⁶ m/s. If the mass of the electron is 9.0 x 10^-31 kg, find its angular momentum.

[Ans. 1.05 x 10^-34 kg m²/s

12. Find the angular momentum of Neptune about the sun. Given distance of Neptune from the sun is 5 x 10¹² m. period of revolution about the sun = 5 x 10⁹s and mass of Neptune = 10²⁷ kg. [Ans. 3.14 x 10⁴³ kg m²I

Date: 2015-01-12; view: 1046