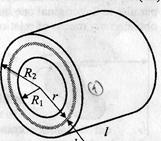
Hollow or solid cylinder

Fig. 38 shows a hollow cylinder of length 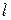and inner and outer radii and . We choose as the most convenient volume element a thin cylindrical sheet of radius 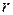, thickness and length 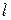. The volume of this shell is very nearly equal to that of flat sheet of thickness , length 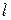, and width 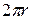. Then

.

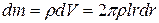The moment of inertia is given by

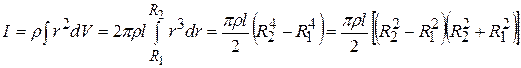
Volume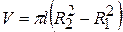

Hence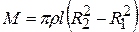

and the moment of inertia is

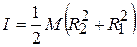
If the cylinder is solid 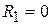letting outer radius be we find that the moment of inertia of a solid cylinder of radius is

If the cylinder is very thin, and 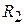, are nearly equal, if represents this common radius

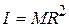(76)

Note, that the moment of inertia of cylinder does not depend on the length 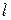. It depends only on the radial distribution of mass, not on distribution along the axis.

5.3.3. Uniform sphere of radius , axis through center

Divide the sphere into thin disks. The radius 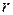of the disk shown in Fig. 7 is

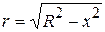
Its volume is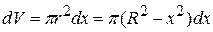

and its mass is .

Hence from Eq. ()

Integrating this expression from 0 to gives the moment of inertia of the right hemisphere. From symmetry, the total 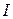for the entire sphere is just twice this:

Carrying out the integration, we obtain

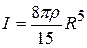
The mass of the sphere is .

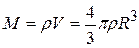Hence .

Torque

A doorknob is located as far as possible from the door's hinge line for a good reason. If you want to open a heavy door, you must certainly apply a force; that alone, however, is not enough. Where you apply that force and in what direction you push are also important. If you apply your force nearer to the hinge line than the knob, or at any angle other than 90° to the plane of the door, you must use a greater force to move the door than if you apply the force at the knob and perpendicular to the door's plane.

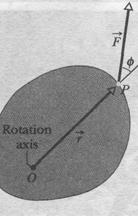
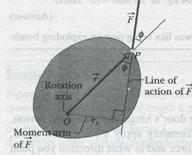
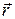Figure 11-15a shows a cross section of a body that is free to rotate about an axis passing through О and perpendicular to the cross section. A force is applied at point P, whose position relative to О is defined by a position vector . The directions of vectors and 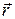make an angle 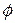with each other. (For simplicity, we consider only forces that have no component parallel to the rotation axis; thus, is in the plane of the page.)

To determine how results in a rotation of the body around the rotation axis, we resolve into two components (Fig. 11-15b). One component, called the radial component , points along 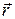. This component does not cause rotation, because it acts along a line that extends through O. (If you pull on a door parallel to the plane of the door, you do not rotate the door.) The other component of tangential component 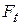, is perpendicular to 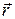and has magnitude . This component does cause rotation. (If you pull on a door perpendicular to its plane, you can rotate the door.)

The ability of to rotate the body depends not only on the magnitude of its tangential component 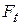, but also on just how far from О the force is applied. To include both these factors, we define a quantity called torque as the product of the two factors and write it as

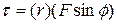
equivalent ways of computing the torque are

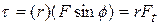
And 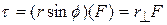, where 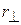is the perpendicular distance between the rotation axis at О and an extended line running through the vector (Fig. 11-15c). This extended line is

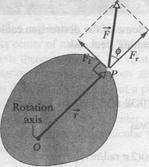
called the line of action of , and 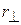is called the moment arm of . Figure 11-15b shows that we can describe 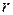, the magnitude of 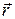, as being the moment arm of the force component .

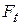Torque, which comes from the Latin word meaning "to twist," may be loosely identified as the turning or twisting action of the force . When you apply a force to an object - such as a screwdriver or torque wrench - with the purpose of turning that object, you are applying a torque. The SI unit of torque is the newton-meter (N • m). Caution: The newton-meter is also the unit of work.

Torque and work, however, are quite different quantities and must not be confused. Work is often expressed in joules (1 J = IN- m), but torque never is.

In the next chapter we shall discuss torque in a general way as being a vector quantity. Here, however, because we consider only rotation around a single axis, we do not need vector notation. Instead, a torque has either a positive or negative value depending on the direction of rotation it would give a body initially at rest: If the body would rotate counterclockwise, the torque is positive. If the object would rotate clockwise, the torque is negative. (The phrase "clocks are negative" from Section 11-2 still works.)

Torques obey the superposition principle that we discussed in Chapter 5 for forces: When several torques act on a body, the net torque (or resultant torque) is the sum of the individual torques. The symbol for net torque is .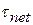

11-9 Newton's Second Law for Rotation

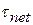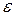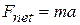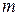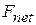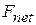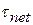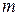A torque can cause rotation of a rigid body, as when you use a torque to rotate a door. Here we want to relate the net torque on a rigid body to the angular acceleration it causes about a rotation axis. We do so by analogy with Newton's second law ( ) for the acceleration a of a body of mass due to a net force along a coordinate axis. We replace with , with 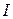, and 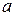with 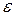, writing

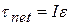(Newton's second law for rotation), 11-34

where 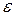must be in radian measure.

Proof of Equation 11-34

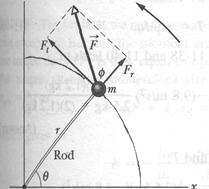
We prove Eq. 11-34 by first considering the simple situation shown in Fig. 11-16.

The rigid body there consists of a particle of mass 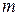on one end of a massless rod of length 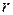. The rod can move only by rotating about its other end, around a rotation axis (an axle) that is perpendicular to the plane of the page. Thus, the particle can move only in a circular path that has the rotation axis at its center.

A force acts on the particle. However, because the particle can move only along the circular path, only the tangential component 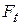of the force (the component that is tangent to the circular path) can accelerate the particle along the path. We can relate 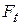to the particle's tangential acceleration along the path with Newton's second law, writing

.

The torque acting on the particle is, from Eq. 11-32,

.

From Eq. 11-22 ( 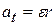) we can write this as

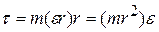11-35

The quantity in parentheses on the right side of Eq. 11-35 is the rotational inertia of the particle about the rotation axis (see Eq. 11-26). Thus, Eq. 11-35 reduces to

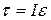
For the situation in which more than one force is applied to the particle, we can generalize Eq. 11-26 as

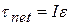
which we set out to prove. We can extend this equation to any rigid body rotating about a fixed axis, because any such body can always be analyzed as an assembly of single particles.

Date: 2015-01-12; view: 1615