Reading a Potential Energy Curve

Once again we consider a particle that is part of a system in which a conservative force acts. This time suppose that the particle is constrained to move along an x axis while the conservative force does work on it. We can learn a lot about the motion of the particle from a plot of the system's potential energy U(x). However, before we discuss such plots, we need one more relationship.

Finding the Force Analytically

Equation 8-6 tells us how to find the change in potential energy between two points in a one-dimensional situation if we know the force . Now we want to go the other way; that is, we know the potential energy function 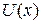and want to find the force.

For one-dimensional motion, the work 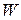done by a force that acts on a particle as the particle moves through a distance 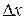is 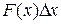. We can then write Eq. 8-1 as

.

Solving for and passing to the differential limit yield

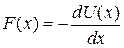(one-dimensional motion).-- (8-20)

-which is the relation we sought.

We can check this result by putting 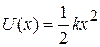, which is the elastic potential energy function for a spring force. Equation 8-20 then yields, as expected, , which is Hooke's law. Similarly, we can substitute 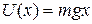, which is the gravitational potential energy function for a particle-Earth system, with a particle of mass m at height x above Earth's surface. Equation 8-20 then yields 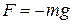, which is the gravitational force on the particle.

The Potential Energy Curve

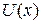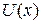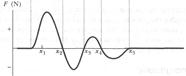
Figure 8-10a is a plot of a potential energy function for a system in which a particle is in one-dimensional motion while a conservative force does work on it. We can easily find by (graphically) taking the slope of the curve at various points. (Equation 8-20 tells us that is negative the slope of the 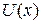curve.) Figure S-lOb is a plot of found in this way.

Date: 2015-01-12; view: 1249